题目内容
设曲线y=x3与直线y=x所围成的封闭区域的面积为S，则下列等式成立的是（ ）
A、S=
| ||
B、S=
| ||
C、S=
| ||
D、S=2
|
考点：定积分的简单应用
专题：导数的概念及应用
分析：作出两个曲线的图象，求出它们的交点，由此可得所求面积为函数x3-x在区间[0，1]上的定积分的值的2倍，再用定积分计算公式加以运算即可得到本题答案．
解答：
解：∵曲线y=x3和曲线y=x的交点为
A（1，1）、原点O和B（-1，-1）
∴由定积分的几何意义，可得所求图形的面积为
S=2
(x-x3)dx．
故选：D．
A（1，1）、原点O和B（-1，-1）∴由定积分的几何意义，可得所求图形的面积为
S=2
| ∫ | 1 0 |
故选：D．
点评：本题求两条曲线围成的曲边图形的面积，着重考查了定积分的几何意义和积分计算公式等知识，属于基础题．
练习册系列答案
相关题目
已知sin（α-β）cosα-cos（α-β）sinα=
，且β为第三象限角．则cosβ等于（ ）
| 7 |
| 25 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
如图，AB是的直径，PB，PE分别切⊙O于B，C，∠ACE=40°，则∠P=（ ）
| A、60° | B、70° |
| C、80° | D、90° |
学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座，每科一节课，每节至少有一科，且数学、理综不安排在同一节，则不同的安排方法共有（ ）
| A、36种 | B、30种 |
| C、24种 | D、6种 |
已知l是直线，α、β是两个不同平面，下列命题中的真命题是（ ）
| A、若l∥α，l∥β，则α∥β |
| B、若α⊥β，l∥α，则l⊥β |
| C、若l⊥α，l∥β，则α⊥β |
| D、若l∥α，α∥β，则l∥β |
若{an}为等差数列，Sn是其前n项和，且S11=
，则tana6=（ ）
| 88π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
一个几何体的三视图及尺寸如图所示，则该几何体的体积为（ ）
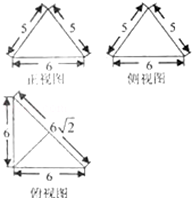
| A、48 | B、72 | C、12 | D、24 |
复数z满足：z（1+i2013）=i2014（i是虚数单位），则复数z在复平面内位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |