题目内容
5.设$x∈(0,\frac{π}{2})$,则函数$y=\frac{sin2x}{{2{{sin}^2}x+1}}$的最大值为$\frac{\sqrt{3}}{3}$.分析 变形可得2x∈(0,π),y=-$\frac{sin2x-0}{cos2x-2}$,表示点(cos2x,sin2x)和(2,0)连线斜率的相反数,点(cos2x,sin2x)在单位圆的上半圆,数形结合可得.
解答 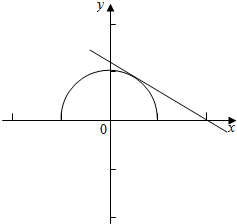 解:∵$x∈(0,\frac{π}{2})$,∴2x∈(0,π),
解:∵$x∈(0,\frac{π}{2})$,∴2x∈(0,π),
变形可得y=$\frac{sin2x}{1-cos2x+1}$=-$\frac{sin2x-0}{cos2x-2}$,
表示点(cos2x,sin2x)和(2,0)连线斜率的相反数,
而点(cos2x,sin2x)在单位圆的上半圆,
结合图象可得当直线倾斜角为150°(相切)时,
函数取最大值-tan150°=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{{\sqrt{3}}}{3}$.
点评 本题考查三角函数的最值,转化为斜率并数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
15.已知过点C(6,-8)作圆x2+y2=25的切线,切点分别为A,B,那么点C到直线AB的距离为( )
| A. | 15 | B. | 10 | C. | $\frac{15}{2}$ | D. | 5 |
16.已知函数f(x)=|x+1|+|x-1|,则下列坐标表示的点一定在函数f(x)图象上的是( )
| A. | (-a,-f(a)) | B. | (-a,f(a)) | C. | (a,-f(a)) | D. | (a,-f(-a)) |
17.集合M={y|y=lg(x2+1),N={x|2x<4},则M∩N等于( )
| A. | [0,+∞) | B. | [0,2) | C. | (2,+∞) | D. | (0,2] |
15.已知某班某个小组6名成员在一次月考中物理成绩如茎叶图所示(图1),本小组的平均成绩为$\overline{x}$,现将各人分数依次输入如图2程序中,则计算输出的结果为( )


| A. | $\sqrt{53}$ | B. | 53 | C. | 80 | D. | 318 |