题目内容
已知函数f(x)=ex-bx,g(x)=|f(x)|,其中e为自然对数的底数.
(Ⅰ)当b=1时,求函数y=f(x)的最小值.
(Ⅱ)若函数y=f(x)有且仅有一个零点,求实数b的取值范围.
(Ⅲ)当b>0时,判断函数y=g(x)在区间(0,2)上是否存在极大值,若存在,求出极大值及相应实数b的取值范围;若不存在,请说明理由.
(Ⅰ)当b=1时,求函数y=f(x)的最小值.
(Ⅱ)若函数y=f(x)有且仅有一个零点,求实数b的取值范围.
(Ⅲ)当b>0时,判断函数y=g(x)在区间(0,2)上是否存在极大值,若存在,求出极大值及相应实数b的取值范围;若不存在,请说明理由.
考点:利用导数求闭区间上函数的最值,函数零点的判定定理,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)先求出函数的导涵数f'(x),在函数的定义域内解不等式f'(x)>0和f'(x)<0,即可求出函数最小值;
(Ⅱ)先将原问题转化为y=ex与y=bx的图象只有一个交点的问题,再对b进行分类讨论:当b<0时,作出图象,发现满足要求;当b≥0时,作出图象,发现当且仅当y=ex与y=bx相切时有一个交点.从而求出实数b的取值范围;
(Ⅲ)求出f'(x)=ex-b,令f'(x)=ex-b=0,则x=lnb,不等式f'(x)>0和f'(x)<0,即可求出函数的单调区间,然后根据极值的定义进行判定极值即可.
(Ⅱ)先将原问题转化为y=ex与y=bx的图象只有一个交点的问题,再对b进行分类讨论:当b<0时,作出图象,发现满足要求;当b≥0时,作出图象,发现当且仅当y=ex与y=bx相切时有一个交点.从而求出实数b的取值范围;
(Ⅲ)求出f'(x)=ex-b,令f'(x)=ex-b=0,则x=lnb,不等式f'(x)>0和f'(x)<0,即可求出函数的单调区间,然后根据极值的定义进行判定极值即可.
解答:
 解:(I)当b=1时f(x)=ex-x,
解:(I)当b=1时f(x)=ex-x,
∴f'(x)=ex-1,
令f'(x)=0,得x=0,
当f'(x)>0,即x>0,
当f'(x)<0,即x<0
∴f(x)的单调递减区间为(-∞,0),单调递增区间为(0,+∞);
故当x=0时,函数有极小值,也是最小值,最小值为f(0)=1,
(Ⅱ)转化为y=ex与y=bx的图象只有一个交点
当b<0时,作出图象,发现满足要求;
当b≥0时,作出图象,
发现当且仅当y=ex与y=bx相切时有一个交点
设切点为(x,y),则
,解得
所以,b<0或b=e,
(Ⅲ)f(x)=ex-bx,f'(x)=ex-b,令f'(x)=ex-b=0,则x=lnb,
当x∈(-∞,lnb)时,f'(x)=ex-b<0,所以f(x)递减;
当x∈(lnb,+∞)时,f'(x)=ex-b>0,所以f(x)递增;
所以,f(x)的最小值为f(lnb)=b-blnb=b(1-lnb);
当0<b≤e时,f(lnb)=b(1-lnb)≥0,所以f(x)=ex-bx≥0,
∴g(x)=|f(x)|=f(x)=ex-bx,
此时,|f(x)|在(-∞,+∞)上无极大值,所以在(0,2)上无极大值;
当b>e时,f(lnb)=b(1-lnb)<0,
∴g(x)=
,
可得:
若b≥e2,则lnb≥2,此时|f(x)|在(0,2)上无极大值;
若b<e2,则lnb<2,此时|f(x)|在(0,2)上有极大值|f(lnb)|=b(lnb-1);
综上得:
当0<b≤e或b≥e2时,|f(x)|在(0,2)上无极大值;
当e<b<e2时,|f(x)|在(0,2)上有极大值|f(lnb)|=b(lnb-1)
 解:(I)当b=1时f(x)=ex-x,
解:(I)当b=1时f(x)=ex-x,∴f'(x)=ex-1,
令f'(x)=0,得x=0,
当f'(x)>0,即x>0,
当f'(x)<0,即x<0
∴f(x)的单调递减区间为(-∞,0),单调递增区间为(0,+∞);
故当x=0时,函数有极小值,也是最小值,最小值为f(0)=1,
(Ⅱ)转化为y=ex与y=bx的图象只有一个交点
当b<0时,作出图象,发现满足要求;
当b≥0时,作出图象,
发现当且仅当y=ex与y=bx相切时有一个交点
设切点为(x,y),则
|
|
所以,b<0或b=e,
(Ⅲ)f(x)=ex-bx,f'(x)=ex-b,令f'(x)=ex-b=0,则x=lnb,
当x∈(-∞,lnb)时,f'(x)=ex-b<0,所以f(x)递减;
当x∈(lnb,+∞)时,f'(x)=ex-b>0,所以f(x)递增;
所以,f(x)的最小值为f(lnb)=b-blnb=b(1-lnb);
当0<b≤e时,f(lnb)=b(1-lnb)≥0,所以f(x)=ex-bx≥0,
∴g(x)=|f(x)|=f(x)=ex-bx,
此时,|f(x)|在(-∞,+∞)上无极大值,所以在(0,2)上无极大值;
当b>e时,f(lnb)=b(1-lnb)<0,
∴g(x)=
|
可得:
若b≥e2,则lnb≥2,此时|f(x)|在(0,2)上无极大值;
若b<e2,则lnb<2,此时|f(x)|在(0,2)上有极大值|f(lnb)|=b(lnb-1);
综上得:
当0<b≤e或b≥e2时,|f(x)|在(0,2)上无极大值;
当e<b<e2时,|f(x)|在(0,2)上有极大值|f(lnb)|=b(lnb-1)
点评:本题考查导数知识的运用,考查函数的单调性,考查导数的几何意义,考查函数的极值,考查分类讨论的数学思想,难度较大

练习册系列答案
相关题目
直线y=x-1与双曲线x2-
=1(b>0)有两个不同的交点,则此双曲线离心率的范围是( )
| y2 |
| b2 |
A、(1,
| ||||
B、(
| ||||
| C、(1,+∞) | ||||
D、(1,
|
设F1,F2为双曲线C:
-
=1(a>0,b>0)的左、右焦点,且直线y=2x为双曲线C的一条渐近线,点P为C上一点,如果|PF1|-|PF2|=4,那么双曲线C的方程为 ;离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
若a是从集合{1,2,3,4}中随机抽取的一个数,b是从集合{1,2,3}中抽取的一个数,则关于x的方程x2+2ax+b2=0有实数根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某电商在“双十一”期间用电子支付系统进行商品买卖,全部商品共有n类(n∈N*),分别编号为1,2,…,n,买家共有m名(m∈N*,m<n),分别编号为1,2,…,m.若aij=
1≤i≤m,1≤j≤n,则同时购买第1类和第2类商品的人数是( )
|
| A、a11+a12+…+a1m+a21+a22+…+a2m |
| B、a11+a21+…+am1+a12+a22+…+am2 |
| C、a11a12+a21a22+…+am1am2 |
| D、a11a21+a12a22+…+a1ma2m |
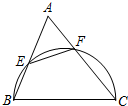 如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么
如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么