题目内容
14.已知长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=4,E为侧面AA1B1B的中心,F为A1D1的中点,求下列向量的数量积:(1)$\overrightarrow{BC}$•$\overrightarrow{E{D}_{1}}$;
(2)$\overrightarrow{BF}$•$\overrightarrow{A{B}_{1}}$;
(3)$\overrightarrow{EF}$•$\overrightarrow{F{C}_{1}}$.
分析 以A为坐标原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,求出A,B,C,A1,B1,C1,D1,E,F的坐标,再由向量的坐标公式,结合向量的数量积的坐标表示,计算可得所求向量的数量积.
解答 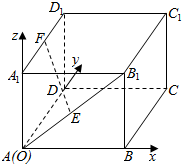 解:如图,以A为坐标原点,AB为x轴,AD为y轴,AA1为z轴,
解:如图,以A为坐标原点,AB为x轴,AD为y轴,AA1为z轴,
建立空间直角坐标系,
即有A(0,0,0),B(2,0,0),C(2,4,0),A1(0,0,2),
B1(2,0,2),C1(2,4,2),D1(0,4,2),
E(1,0,1),F(0,2,2),
(1)$\overrightarrow{BC}$•$\overrightarrow{E{D}_{1}}$=(0,4,0)•(-1,4,1)=0×(-1)+4×4+0×1=16;
(2)$\overrightarrow{BF}$•$\overrightarrow{A{B}_{1}}$=(-2,2,2)•(2,0,2)=-2×2+2×0+2×2=0;
(3)$\overrightarrow{EF}$•$\overrightarrow{F{C}_{1}}$=(-1,2,1)•(2,2,0)=-1×2+2×2+1×0=2.
点评 本题考查空间向量的数量积的坐标表示,考查运算能力,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
4.已知是等差数列{an},且a2+a8=16,则数列{an}的前9项和等于( )
| A. | 36 | B. | 72 | C. | 144 | D. | 288 |
5.已知sin(π+a)=$\frac{1}{2}$,则sin(9π+a)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
19.若点p在抛物线y2=2x上,A(a,0)
(1)请你完成下表:
(2)若α∈R,求|PA|的最小值及相应的点P坐标.
(1)请你完成下表:
| 实物a的值 | -2 | 0 | 0.5 | 1 | 2 |
| |PA|的最小值 | 0 | ||||
| 相应的点P坐标 |