题目内容
已知圆C:(x+1)2+(y+1)2=1,点P(x0,y0)在直线x-y+2=0上.若圆C上存在点Q使∠CPQ=30°,则x0的取值范围是 .
考点:点与圆的位置关系
专题:直线与圆
分析:取点P(-1,1)时,可得PQ与圆相切时满足∠CPQ=30°;取点P(-3,-1)时,可得PQ与圆相切时满足∠CPQ=30°.进而得出答案.
解答:
 解:如图所示,
解:如图所示,
①当x0=-1,y0=1时,即取点P(-1,1)时,可得PQ与圆相切时满足∠CPQ=30°;
②当x0=-3,y0=-1时,即取点P(-3,-1)时,可得PQ与圆相切时满足∠CPQ=30°.
综上可知:只有当-3≤x0≤-1时,满足圆C上存在点Q使∠CPQ=30°.
故答案为:[-3,-1].
 解:如图所示,
解:如图所示,①当x0=-1,y0=1时,即取点P(-1,1)时,可得PQ与圆相切时满足∠CPQ=30°;
②当x0=-3,y0=-1时,即取点P(-3,-1)时,可得PQ与圆相切时满足∠CPQ=30°.
综上可知:只有当-3≤x0≤-1时,满足圆C上存在点Q使∠CPQ=30°.
故答案为:[-3,-1].
点评:本题考查了直线与圆相切的性质、斜率计算公式、数形结合思想方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,BC=3,AC=
,B=
,则△ABC的面积是( )
| 13 |
| π |
| 3 |
A、3
| ||||
B、6
| ||||
C、
| ||||
D、
|
已知i是虚数单位,且z=(
)2014+i的共轭复数为
,则z•
等于( )
| 1-i |
| 1+i |
. |
| z |
. |
| z |
| A、2 | B、1 | C、0 | D、-1 |
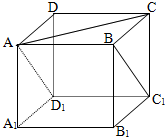 如图,正方体ABCD-A1B1C1D1中,点P是直线BC1的动点,则下列四个命题:
如图,正方体ABCD-A1B1C1D1中,点P是直线BC1的动点,则下列四个命题: