题目内容
已知数列{an}的前n项和Sn=
an-
×3n+1+
,求数列{an}的通项公式.
| 9 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出
+1=3(
+1),a1=6.由此能求出数列{an}的通项公式.
| an |
| 3n |
| an-1 |
| 3n |
解答:
解:∵Sn=
an-
×3n+1+
,
∴Sn-1=
an-1-
×3n+
,n≥2
∴an=Sn-Sn-1=
an-
an-1-
×3n,
整理,得an=9an-1+2•3n,
∴
+1=3(
+1),
∵a1=S1=
a1-
×32+
,解得a1=6.
∴
+1=3,
∴{
+1}是首项为3,公比为3的等比数列,
∴
+1=3n,
∴an=32n-3n.
| 9 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
∴Sn-1=
| 9 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
∴an=Sn-Sn-1=
| 9 |
| 8 |
| 9 |
| 8 |
| 1 |
| 4 |
整理,得an=9an-1+2•3n,
∴
| an |
| 3n |
| an-1 |
| 3n |
∵a1=S1=
| 9 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
∴
| a1 |
| 3 |
∴{
| an |
| 3n |
∴
| an |
| 3n |
∴an=32n-3n.
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
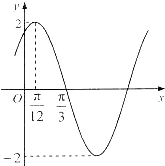
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
)的部分图象如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||||
B、ω=
| ||||
C、ω=2,φ=
| ||||
D、ω=
|
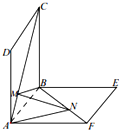 如图正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<