题目内容
已知椭圆 :
: 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,且
的焦点相同,且 的离心率
的离心率 ,又
,又 为椭圆的左右顶点,
为椭圆的左右顶点, 其上任一点(异于
其上任一点(异于 ).
).
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线 交直线
交直线 于点
于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 轴于点
轴于点 ,求
,求 的坐标;
的坐标;
(Ⅲ)求点 在直线
在直线 上射影的轨迹方程.
上射影的轨迹方程.
 :
: 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,且
的焦点相同,且 的离心率
的离心率 ,又
,又 为椭圆的左右顶点,
为椭圆的左右顶点, 其上任一点(异于
其上任一点(异于 ).
).(Ⅰ)求椭圆的方程;
(Ⅱ)若直线
 交直线
交直线 于点
于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 轴于点
轴于点 ,求
,求 的坐标;
的坐标;(Ⅲ)求点
 在直线
在直线 上射影的轨迹方程.
上射影的轨迹方程.(1)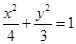 ;(2)
;(2)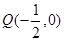 ;(3)
;(3)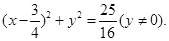
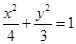 ;(2)
;(2)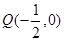 ;(3)
;(3)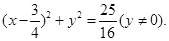
(1) 由题意知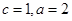 ,易知椭圆方程为
,易知椭圆方程为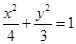
(2)本小题的求解要注意利用平面几何的性质得到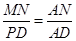 ,另外要注意应用
,另外要注意应用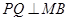 ,点M在椭圆上等几何要素建立方程求解即可.
,点M在椭圆上等几何要素建立方程求解即可.
(3) 点 在直线
在直线 上射影即PQ与MB的交点H,由
上射影即PQ与MB的交点H,由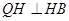 得
得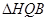 为直角三角形,设E为
为直角三角形,设E为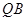 中点,则
中点,则 =
=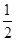
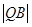 =
=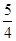 ,
,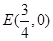 ,因此H点的轨迹是以E为圆心,半径为
,因此H点的轨迹是以E为圆心,半径为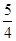 的圆去掉与x轴的交点.解:(Ⅰ)由题意知
的圆去掉与x轴的交点.解:(Ⅰ)由题意知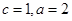 ,故椭圆方程为
,故椭圆方程为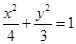 ..........3分
..........3分
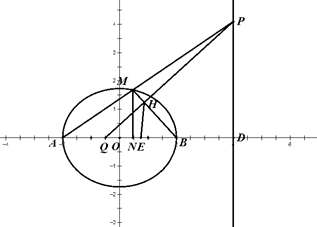
(Ⅱ)设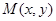 ,
,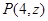 则由图知
则由图知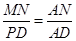 ,得
,得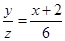 ,故
,故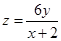 .
.
设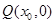 ,由
,由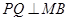 得:
得: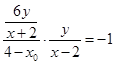 ,
,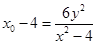 .
.
又 在椭圆上,故
在椭圆上,故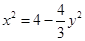 ,化简得
,化简得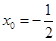 ,即
,即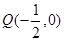 ...............8分
...............8分
(Ⅲ)点 在直线
在直线 上射影即PQ与MB的交点H,由
上射影即PQ与MB的交点H,由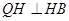 得
得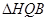 为直角三角形,设E为
为直角三角形,设E为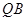 中点,则
中点,则 =
=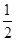
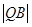 =
=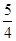 ,
,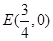 ,因此H点的轨迹方程为
,因此H点的轨迹方程为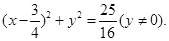 ...................13分
...................13分
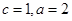 ,易知椭圆方程为
,易知椭圆方程为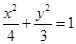
(2)本小题的求解要注意利用平面几何的性质得到
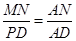 ,另外要注意应用
,另外要注意应用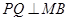 ,点M在椭圆上等几何要素建立方程求解即可.
,点M在椭圆上等几何要素建立方程求解即可.(3) 点
 在直线
在直线 上射影即PQ与MB的交点H,由
上射影即PQ与MB的交点H,由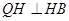 得
得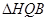 为直角三角形,设E为
为直角三角形,设E为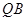 中点,则
中点,则 =
=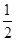
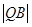 =
=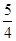 ,
,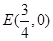 ,因此H点的轨迹是以E为圆心,半径为
,因此H点的轨迹是以E为圆心,半径为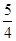 的圆去掉与x轴的交点.解:(Ⅰ)由题意知
的圆去掉与x轴的交点.解:(Ⅰ)由题意知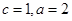 ,故椭圆方程为
,故椭圆方程为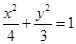 ..........3分
..........3分
(Ⅱ)设
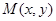 ,
,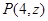 则由图知
则由图知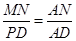 ,得
,得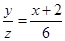 ,故
,故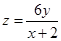 .
.设
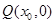 ,由
,由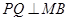 得:
得: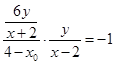 ,
,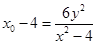 .
.又
 在椭圆上,故
在椭圆上,故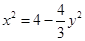 ,化简得
,化简得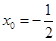 ,即
,即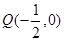 ...............8分
...............8分(Ⅲ)点
 在直线
在直线 上射影即PQ与MB的交点H,由
上射影即PQ与MB的交点H,由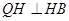 得
得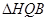 为直角三角形,设E为
为直角三角形,设E为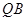 中点,则
中点,则 =
=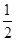
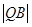 =
=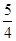 ,
,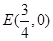 ,因此H点的轨迹方程为
,因此H点的轨迹方程为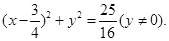 ...................13分
...................13分
练习册系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为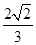 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
. 为椭圆
为椭圆 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )



 :
: (
( ),直线
),直线 为圆
为圆 :
: 的一条切线并且过椭圆的右焦点,记椭圆的离心率为
的一条切线并且过椭圆的右焦点,记椭圆的离心率为 .
. ,求
,求 的右焦点为
的右焦点为 ,点
,点 在圆
在圆 上任意一点(点
上任意一点(点 的切线交椭圆
的切线交椭圆 于两点
于两点 、
、 .
. ;
;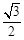 ,求线段
,求线段 长度的最大值.
长度的最大值.
 的离心率为
的离心率为 ,且过点
,且过点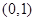 ,过
,过 的右焦点
的右焦点 任作直线
任作直线 ,设
,设 ,
, 两点(异于
两点(异于 ,
, ,记
,记 .
.
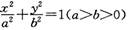 的左、右顶点,C(0,b),直线
的左、右顶点,C(0,b),直线 与X轴交于点D,与直线AC交于点P,且BP平分
与X轴交于点D,与直线AC交于点P,且BP平分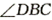 ,则此椭圆的离心率为
,则此椭圆的离心率为 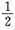
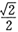

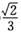
 的左、右焦点分别为F1,F2,过F2作
的左、右焦点分别为F1,F2,过F2作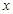 轴的垂线与
轴的垂线与 ,则椭圆的离心率
,则椭圆的离心率 。
。 的焦距为
的焦距为 ,则实数
,则实数 .
.