题目内容
16.若抛物线y2=2px(p>0)的准线经过椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的一个焦点,则该抛物线的准线方程为x=-2.分析 先求出椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的焦点为F1(-2,0),F2(2,0),由此能过河卒子 同该抛物线的准线方程.
解答 解:椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的焦点为F1(-2,0),F2(2,0),
∵抛物线y2=2px(p>0)的准线经过椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的一个焦点,
∴该抛物线的准线方程为x=-2.
故答案为:x=-2.
点评 本题考查抛物线的准线方程的求法,是基础题,解题时要认真审题,注意椭圆、抛物线的性质的合理运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
8.已知等差数列{an}的前15项之和为$\frac{15π}{4}$,则tan(a7+a8+a9)=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
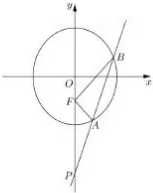 如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P
如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P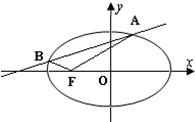 已知点P是椭圆C上的任一点,P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且$\frac{{d}_{2}}{{d}_{1}}$=$\frac{\sqrt{2}}{2}$.
已知点P是椭圆C上的任一点,P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且$\frac{{d}_{2}}{{d}_{1}}$=$\frac{\sqrt{2}}{2}$.