题目内容
已知曲线y=
在点P（1，4）处的切线与直线l平行且距离为
，则直线l的方程为（ ）
| 4 |
| x |
| 17 |
| A、4x-y+9=0或4x-y+25=0 |
| B、4x-y+9=0 |
| C、4x+y+9=0或4x+y-25=0 |
| D、以上都不对 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求出曲线y=
在点P（1，4）处的切线方程，再求出与直线l平行且距离为
的直线l的方程．
| 4 |
| x |
| 17 |
解答：
解：因为曲线y=
，所以y′=-
，
所以在点P（1，4）处的切线的斜率为-4，方程为4x+y-8=0，
与直线l平行且距离为
的直线方程为4x+y+c=0，则
=
，
所以c=9或-25，
因此直线的方程为4x+y+9=0或4x+y-25=0，
故选C．
| 4 |
| x |
| 4 |
| x2 |
所以在点P（1，4）处的切线的斜率为-4，方程为4x+y-8=0，
与直线l平行且距离为
| 17 |
| |c+8| | ||
|
| 17 |
所以c=9或-25，
因此直线的方程为4x+y+9=0或4x+y-25=0，
故选C．
点评：本题考查利用导数研究曲线上某点切线方程，考查直线方程，考查学生的计算能力，比较基础．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
在同一直角坐标系中，函数f（x）=logax（a＞0，a≠1）与函数g（x）=ax（a＞0，a≠1）的图象可能是（ ）
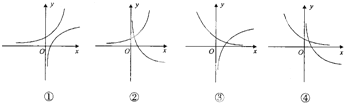
| A、①② | B、①③ | C、①④ | D、②④ |
函数f（x）=
的定义域为（ ）
| 2x-1 |
| log3x |
| A、（0，+∞） |
| B、（1，+∞） |
| C、（0，1） |
| D、（0，1）∪（1，+∞） |