题目内容
19.已知数列{an}满足a1=1,a2=4,且对任意m,n,p,q∈N*,若m+n=p+q,则有am+an=ap+aq.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为Sn,求证:$\frac{1}{4}$≤Sn<$\frac{1}{3}$.
分析 (I)令m=1,p=n-1,q=2,可得:an+a1=an-1+a2,即an-an-1=3.(n≥2).利用等差数列的通项公式即可得出.
(II)$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}(\frac{1}{3n-2}-\frac{1}{3n+1})$.利用裂项求和方法与数列的单调性即可证明.
解答 (I)解:令m=1,p=n-1,q=2,可得:an+a1=an-1+a2,即an-an-1=3.(n≥2).
∴数列{an}是等差数列,公差为3.
∴an=1+3(n-1)=3n-2.
(II)证明:$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}(\frac{1}{3n-2}-\frac{1}{3n+1})$.
∴Sn=$\frac{1}{3}[(1-\frac{1}{4})$+$(\frac{1}{4}-\frac{1}{7})$+…+$(\frac{1}{3n-2}-\frac{1}{3n+1})]$
=$\frac{1}{3}$$(1-\frac{1}{3n+1})$<$\frac{1}{3}$.
另一方面:数列$\{-\frac{1}{3n+1}\}$单调递增,∴Sn≥S1=$\frac{1}{4}$.
∴$\frac{1}{4}$≤Sn<$\frac{1}{3}$.
点评 本题考查了数列递推关系、等差数列的通项公式、裂项求和方法、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
14.在区间[-2,4]上随机地取一个数x,使${a^2}+\frac{1}{{{a^2}+1}}≥|x|$恒成立的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
4.曲线y=$\frac{1}{4}{x^2}$在点(2,1)处的切线与x轴、y轴围成的封闭图形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
11.若a∈R,则复数z=$\frac{3-ai}{i}$在复平面内对应的点在第三象限是a≥0的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.已知集合A={x|0<x<2},B={x|x2-1<0},则A∪B=( )
| A. | (-1,1) | B. | (-1,2) | C. | (1,2) | D. | (0,1) |

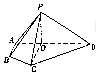 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.