题目内容
2.当x=θ时,函数f(x)=sinx+$\sqrt{3}$cosx取得最大值,则cosθ=$\frac{\sqrt{3}}{2}$.分析 化函数f(x)为正弦型函数,求出f(x)取得最大值时x的值,再计算cosθ的值.
解答 解:函数f(x)=sinx+$\sqrt{3}$cosx
=2($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)
=2sin(x+$\frac{π}{3}$),
当x+$\frac{π}{3}$=$\frac{π}{2}$+2kπ,k∈Z,
即x=$\frac{π}{6}$+2kπ,k∈Z时f(x)取得最大值,
所以cosθ=cos($\frac{π}{6}$+2kπ)=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了三角恒等变换与三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
12.如图程序框图表示的算法运行后,输出的结果是( )


| A. | 25 | B. | 125 | C. | 150 | D. | 250 |
13.下面的程序框图的作用是输出两数中的较大者,则①②处分别为( )


| A. | 输出m;交换m和n的值 | B. | 交换m和n的值;输出m | ||
| C. | 输出n;交换m和n的值 | D. | 交换m和n的值;输出n |
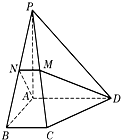 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.