题目内容
13．某三棱锥的三视图如图所示，则该三棱锥四个面的面积中最大的是（ ）
| A． | $\sqrt{5}$ | B． | 3 | C． | $\frac{{3\sqrt{5}}}{2}$ | D． | $3\sqrt{5}$ |
分析 根据三视图作出三棱锥的直观图，计算四个侧面的面积进行比较．
解答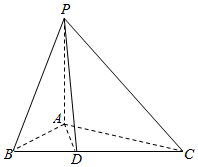 
解：作出三棱锥P-ABC的直观图如图所示，过A作AD⊥BC，垂足为D，连结PD．由三视图可知PA⊥平面ABC，
AB=AD=1，CD=PA=2，∴BC=3，PD=$\sqrt{P{A}^{2}+A{D}^{2}}$=$\sqrt{5}$．AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{5}$，AB=$\sqrt{2}$．BC⊥PD．
∴SABC=$\frac{1}{2}×BC×AD$=$\frac{3}{2}$，S△ABP=$\frac{1}{2}×AB×PA$=$\sqrt{2}$，S△ACP=$\frac{1}{2}×AC×PA$=$\sqrt{5}$，S△BCP=$\frac{1}{2}×BC×PD$=$\frac{3\sqrt{5}}{2}$．
∴三棱锥P-ABC的四个面中，侧面PBC的面积最大．
故选C．
点评 本题考查了棱锥的结构特征和三视图，面积计算，作出直观图是解题关键，属于中档题．
练习册系列答案
核心素养学练评系列答案
相关题目
3．下列函数中，是偶函数且在区间（0，+∞）上单调递减的函数是（ ）
| A． | y=2x | B． | y=$\sqrt{x}$ | C． | y=|x| | D． | y=-x2+1 |
2．设a，b是两条不同直线，下列命题α，β，γ是三个不同平面，下列命题不正确的是（ ）
| A． | b?α，a∥b⇒a∥α | B． | a∥α，α∩β=b，a?β⇒a∥b | ||
| C． | a?α，b?α，a∩b=p，a∥β，b∥β⇒α∥β | D． | α∥β，α∩γ=a，β∩γ=b⇒a∥b |
3．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•（$\overrightarrow{b}$+$\overrightarrow{a}$）=2，且|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{2π}{3}$ |