题目内容
18.已知函数f(x)=x3+ax2,曲线y=f(x)在点P(-1,b)处的切线平行于直线3x+y=0,则切线方程为3x+y+1=0.分析 求出函数的导数,利用导数的几何意义和两直线平行的条件:斜率相等,解方程可得a,b,即可求出切线方程.
解答 解:函数的导数为y′=f′(x)=3x2+2ax,
∵曲线在点P(-1,b)处的切线平行于直线3x+y=0,
∴曲线在点P处的切线斜率k=-3,
即k=f′(-1)=3-2a=-3,
解得a=3,此时f(x)=x3+3x2,
此时b=f(-1)=-1+3=2,
即切点P(-1,2),
则切线方程为y-2=-3(x+1),
即3x+y+1=0
故答案为:3x+y+1=0.
点评 本题主要考查函数的切线方程以及直线平行的斜率关系,利用导数的几何意义求出切线斜率是解决本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
8.执行如图所示的程序框图,若p=0.9,则输出的n为( )


| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
9.下列各角中,与50°的角终边相同的角是( )
| A. | -310° | B. | -50° | C. | 140° | D. | 40° |
13.某三棱锥的三视图如图所示,则该三棱锥四个面的面积中最大的是( )

| A. | $\sqrt{5}$ | B. | 3 | C. | $\frac{{3\sqrt{5}}}{2}$ | D. | $3\sqrt{5}$ |
10. 一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
 一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
8.为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两类:1.到各班做宣传,倡议同学们积极捐献冬衣;2.整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:
(Ⅰ)据此统计,你是否认为志愿者对工作的选择与其性别有关?
(Ⅱ)用分层抽样的方法在从参与整理、打包衣物工作的志愿者中抽取5人,再从这5人中选2人.那么至少有一人是女生的概率是多少?
参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$.
| 到班级宣传 | 整理、打包衣物 | 总计 | |
| 男生 | 12 | 12 | 24 |
| 女生 | 8 | 18 | 26 |
| 总计 | 20 | 30 | 50 |
(Ⅱ)用分层抽样的方法在从参与整理、打包衣物工作的志愿者中抽取5人,再从这5人中选2人.那么至少有一人是女生的概率是多少?
参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$.
| P(X2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
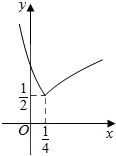 如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).
如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).