题目内容
若α、β为锐角,且cosα=
,sinβ=
,则α+β= .
| 1 | ||
|
| 2 | ||
|
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系求得sinα、cosβ的值,再利用两角和的余弦公式求得cos(α+β)=cosαcosβ-sinαsinβ 的值.
解答:
解:∵α、β为锐角,且cosα=
,sinβ=
,
∴sinα=
=
,cosβ=
=
.
cos(α+β)=cosαcosβ-sinαsinβ=
×
-
×
=-
=-
,
结合0<α+β<π,可得α+β=
,
故答案为:
.
| 1 | ||
|
| 2 | ||
|
∴sinα=
| 1-cos2α |
3
| ||
| 10 |
| 1-sin2β |
| 1 | ||
|
cos(α+β)=cosαcosβ-sinαsinβ=
| 1 | ||
|
| 1 | ||
|
3
| ||
| 10 |
| 2 | ||
|
| 5 | ||
|
| ||
| 2 |
结合0<α+β<π,可得α+β=
| 3π |
| 4 |
故答案为:
| 3π |
| 4 |
点评:本题主要考查同角三角函数的基本关系,两角和的余弦公式的应用,根据三角函数的值求角,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
给定函数y=f(x)的图象如下列图中,经过原点和(1,1),且对任意an∈(0,1),由关系式an+1=f(an)得到数列{an},满足an+1>an(n∈N*),则该函数的图象为( )
A、 |
B、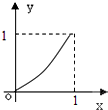 |
C、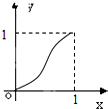 |
D、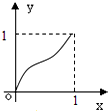 |
若方程
=x+m没有实数根,则实数m的取值范围为( )
1-
|
A、(-∞,-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、(
|
函数f(x)=x2•cosx在区间[-
,
]内的图象大致为( )
| π |
| 2 |
| π |
| 2 |
A、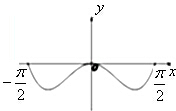 |
B、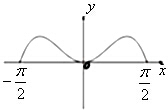 |
C、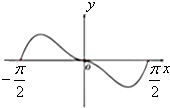 |
D、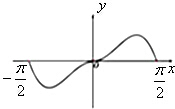 |