题目内容
已知过点(0,
)的直线与圆x2+(y-2)2=1相交于两点A、B,则弦AB中点的轨迹为 .
| 3 |
| 2 |
考点:轨迹方程
专题:直线与圆
分析:根据圆的特殊性,求出圆心为C的坐标,设弦AB中点为M,则有CM⊥AB,当斜率存在时,kCMkAB=-1,斜率不存在时加以验证,最后综合讨论结果,可得答案.
解答:
解:设圆x2+(y-2)2=1的圆心为C,则C的坐标是(0,2),弦AB中点为M(x,y),
由题意,CM⊥AB,
①当直线CM与AB的斜率都存在时,即x≠±
,x≠0时,则有kCMkAB=-1,
∴
×
=-1(x≠0),
化简得x2+y2-
y+3=0(x≠±
,x≠0),
②当x=0时,y=
,点(0,
)适合题意,
③当x=0时,y=2,点(0,2)适合题意,
∴点M的轨迹方程是x2+y2-
y+3=0
由题意,CM⊥AB,
①当直线CM与AB的斜率都存在时,即x≠±
| ||
| 2 |
∴
y-
| ||
| x |
| y-2 |
| x |
化简得x2+y2-
| 7 |
| 2 |
| ||
| 2 |
②当x=0时,y=
| 3 |
| 2 |
| 3 |
| 2 |
③当x=0时,y=2,点(0,2)适合题意,
∴点M的轨迹方程是x2+y2-
| 7 |
| 2 |
点评:本题主要考查轨迹方程的求解,应注意利用圆的特殊性,同时注意所求轨迹的纯粹性,避免增解.

练习册系列答案
相关题目
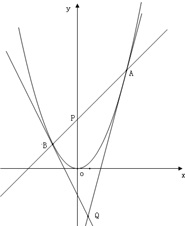 已知A、B为抛物线C:x2=2y上的两点,点P(0,t)(t>0)满足
已知A、B为抛物线C:x2=2y上的两点,点P(0,t)(t>0)满足