Question

若直线y=x+k与曲线y=-

1-(x-3)2

有公共点，则k的取值范围是（　　）

• A、[-3-

  2

  ，-3+

  2

  ]
• B、[-4，-3+

  2

  ]
• C、[-3-

  2

  ，-2]
• D、[-4，-2]

Answer 1

考点：直线与圆的位置关系

专题：直线与圆

分析：曲线y=-

1-(x-3)2

表示一个半圆，如图所示．若直线y=x+k与曲线y=-

1-(x-3)2

有公共点，当直线过点（2，0）时，k取最大值；当直线y=x+k与半圆相切时k有最小值，进而可得答案．

解答： 解：曲线y=-

1-(x-3)2

表示一个半圆，如图所示．

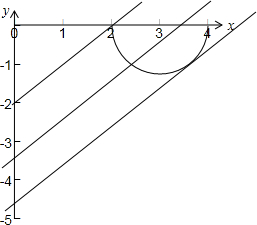
当直线过点（2，0）时，直线y=x+k与半圆只有一个交点，此时k=-2；
当直线y=x+k与半圆相切时只有一个公共点，k=-3-

2

，或k=-3+

2

（舍去），
因此当k∈[-3-

2

，-2]时，直线y=x+k与曲线y=-

1-(x-3)2

有公共点，
故选：C

点评：本题考查了直线与圆的相交于相切的位置关系、数形结合思想方法等基础知识与基本方法，考查了推理能力和计算能力．