题目内容
已知棱长为1的正方体ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点.
①存在P,Q两点,使BP⊥DQ;
②存在P,Q两点,使BP,DQ与直线B1C都成45°的角;
③若|PQ|=1,则四面体BDPQ的体积一定是定值;
④若|PQ|=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.
以上命题为真命题的个数是( )
①存在P,Q两点,使BP⊥DQ;
②存在P,Q两点,使BP,DQ与直线B1C都成45°的角;
③若|PQ|=1,则四面体BDPQ的体积一定是定值;
④若|PQ|=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.
以上命题为真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:令P与A1点重合,Q与C1点重合,可判断①;根据BP与直线B1C所成的角最小值为45°,可判断②;根据平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥(其中O为上底面中心),可判断③;根据四面体BDPQ在该正方体六个面上的正投影的面积不变,可判断④.
解答:
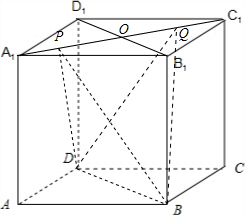 解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故①正确;
解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故①正确;
当P与A1点重合时,BP与直线B1C所成的角最小,此时两异面直线夹角为60°,故②错误;
设平面A1B1C1D1两条对角线交点为O,则易得PQ⊥平面OBD,
平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥,
故四面体BDPQ的体积一定是定值,故③正确;
四面体BDPQ在上下两个底面上的投影是对角线互相垂直且对角线长度均为1的四边形,其面积为定值,
四面体BDPQ在四个侧面上的投影,均为上底为
,下底和高均为1的梯形,其面积为定值,
故四面体BDPQ在该正方体六个面上的正投影的面积的和为定值,故④正确;
故为真命题的有3个.
故选:C
 解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故①正确;
解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故①正确;当P与A1点重合时,BP与直线B1C所成的角最小,此时两异面直线夹角为60°,故②错误;
设平面A1B1C1D1两条对角线交点为O,则易得PQ⊥平面OBD,
平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥,
故四面体BDPQ的体积一定是定值,故③正确;
四面体BDPQ在上下两个底面上的投影是对角线互相垂直且对角线长度均为1的四边形,其面积为定值,
四面体BDPQ在四个侧面上的投影,均为上底为
| ||
| 2 |
故四面体BDPQ在该正方体六个面上的正投影的面积的和为定值,故④正确;
故为真命题的有3个.
故选:C
点评:本题考查的知识点是棱柱的几何特征,是空间异面直线关系,棱锥体积,投影的综合应用,难度较大.

练习册系列答案
相关题目
 已知i为执行如图所示的程序框图输出的结果,则二项式(i
已知i为执行如图所示的程序框图输出的结果,则二项式(i| x |
| 1 | ||
|
| A、192 | B、32 |
| C、-42 | D、-192 |
函数y=-
x2+2x-5的图象的对称轴是( )
| 1 |
| 2 |
| A、直线x=2 |
| B、直线a=-2 |
| C、直线y=2 |
| D、直线x=4 |
对抛物线y=2(x-2)2-3与y=-2(x-2)2+4的说法不正确的是( )
| A、抛物线的形状相同 |
| B、抛物线的顶点相同 |
| C、抛物线对称轴相同 |
| D、抛物线的开口方向相反 |
 如图,椭圆C1:
如图,椭圆C1: 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=