题目内容
 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=| 1 |
| 2 |
(Ⅰ)求证:EG∥平面ABF;
(Ⅱ)求三棱锥B-AEG的体积;
(Ⅲ)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由.
考点:平面与平面垂直的性质,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:
分析:(Ⅰ)取AB中点M,连接MG,则EF∥MG,①即得证.
(Ⅱ)转换三棱锥B-AEG为E-ABG即可求得体积.
(Ⅲ)只要证明AE⊥CDE即可.
(Ⅱ)转换三棱锥B-AEG为E-ABG即可求得体积.
(Ⅲ)只要证明AE⊥CDE即可.
解答:
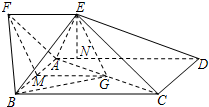 (I)证明:取AB中点M,连FM,GM.
(I)证明:取AB中点M,连FM,GM.
∵G为对角线AC的中点,
∴GM∥AD,且GM=
AD,
又∵FE∥
AD,
∴GM∥FE且GM=FE.
∴四边形GMFE为平行四边形,即EG∥FM.
又∵EG?平面ABF,FM?平面ABF,
∴EG∥平面ABF.…(4分)
(Ⅱ)解:作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED,面ABCD∩面AFED=AD,
得EN⊥平面ABCD,即EN为三棱锥E-ABG的高.
∵在△AEF中,AF=FE,∠AFE=60°,
∴△AEF是正三角形.
∴∠AEF=60°,
由EF∥AD知∠EAD=60°,
∴EN=AE?sin60°=
.
∴三棱锥B-AEG的体积为VB-AEG=VE-ABG=
S△ABG•EN=
×
×2×2×
=
.…(8分)
(Ⅲ)解:平面BAE⊥平面DCE.证明如下:
∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴CD⊥平面AFED,
∴CD⊥AE.
∵四边形AFED为梯形,FE∥AD,且∠AFE=60°,
∴∠FAD=120°.
又在△AED中,EA=2,AD=4,∠EAD=60°,
由余弦定理,得ED=2
.
∴EA2+ED2=AD2,
∴ED⊥AE.
又∵ED∩CD=D,
∴AE⊥平面DCE,
又AE?面BAE,
∴平面BAE⊥平面DCE. …(12分)
 (I)证明:取AB中点M,连FM,GM.
(I)证明:取AB中点M,连FM,GM.∵G为对角线AC的中点,
∴GM∥AD,且GM=
| 1 |
| 2 |
又∵FE∥
| 1 |
| 2 |
∴GM∥FE且GM=FE.
∴四边形GMFE为平行四边形,即EG∥FM.
又∵EG?平面ABF,FM?平面ABF,
∴EG∥平面ABF.…(4分)
(Ⅱ)解:作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED,面ABCD∩面AFED=AD,
得EN⊥平面ABCD,即EN为三棱锥E-ABG的高.
∵在△AEF中,AF=FE,∠AFE=60°,
∴△AEF是正三角形.
∴∠AEF=60°,
由EF∥AD知∠EAD=60°,
∴EN=AE?sin60°=
| 3 |
∴三棱锥B-AEG的体积为VB-AEG=VE-ABG=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
(Ⅲ)解:平面BAE⊥平面DCE.证明如下:
∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴CD⊥平面AFED,
∴CD⊥AE.
∵四边形AFED为梯形,FE∥AD,且∠AFE=60°,
∴∠FAD=120°.
又在△AED中,EA=2,AD=4,∠EAD=60°,
由余弦定理,得ED=2
| 3 |
∴EA2+ED2=AD2,
∴ED⊥AE.
又∵ED∩CD=D,
∴AE⊥平面DCE,
又AE?面BAE,
∴平面BAE⊥平面DCE. …(12分)
点评:本题考查了线面平行的判定,借助体积的计算考查了线面垂直以及面面垂直的判定和性质.

练习册系列答案
相关题目
执行如图所示的程序框图(算法流程图),输出的结果是( )


| A、5 | B、6 | C、7 | D、8 |
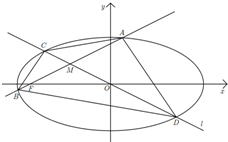 如图,已知椭圆E:
如图,已知椭圆E: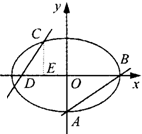 已知椭圆
已知椭圆