题目内容
1．在报名的5名男生和3名女生中，选取5人参加数学竞赛，则男、女生都有的概率为$\frac{55}{56}$．（结果用分数表示）分析 基本事件总数n=${C}_{8}^{5}$=56，男、女生都有的对立事件是选中5名男生，由此利用对立事件概率计算公式能求出男、女生都有的概率．
解答 解：∵在报名的5名男生和3名女生中，选取5人参加数学竞赛，
基本事件总数n=${C}_{8}^{5}$=56，
男、女生都有的对立事件是选中5名男生，
则男、女生都有的概率为p=1-$\frac{{C}_{5}^{5}}{{C}_{8}^{5}}$=$\frac{55}{56}$．
故答案为：$\frac{55}{56}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．
练习册系列答案
相关题目
12．由下列各组命题构成的新命题“p且q”为真命题的是（ ）
| A． | p：4+4=9，q：7＞4 | B． | p：a∈{a，b，c}，q：{a}⊆{a，b，c} | ||
| C． | p：15是质数，q：8是12的约数 | D． | p：2是偶数，q：2不是质数 |
13．已知向量$\overrightarrow a=（1，\sqrt{1+sin{{40}^0}}），\overrightarrow b=（\frac{1}{{sin{{65}^0}}}，x）$共线，则实数x的值为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{2}tan{25°}$ | D． | $\sqrt{3}$ |
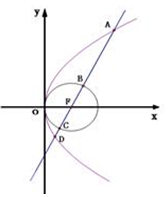圆F：（x-1）2-y2=1和抛物线y2=4x，过F的直线l与抛物线和圆依次交于A、B、C、D四点