题目内容
8.已知圆的方程为x2+y2=8,圆内有一点P(-1,2),AB为过点P且倾斜角为α的弦.(1)当α=135°时,求AB的长
(2)求过点P的弦的中点的轨迹方程.
分析 (1)过点O做OG⊥AB于G,连接OA,依题意可知直线AB的斜率,求得AB的方程,利用点到直线的距离求得OG即圆的半径,进而求得OA的长,则OB可求得.
(2)设出AB的中点的坐标,依据题意联立方程组,消去k求得x和y的关系式,即P的轨迹方程.
解答 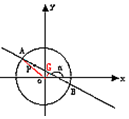 解:(1)过点O做OG⊥AB于G,连接OA,
解:(1)过点O做OG⊥AB于G,连接OA,
当α=135°时,直线AB的斜率为-1,
故直线AB的方程x+y-1=0,
∴|OG|=$\frac{|0+0-1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∵r=2$\sqrt{2}$,
∴|AG|=$\sqrt{8-\frac{1}{2}}$=$\frac{\sqrt{30}}{2}$,
∴|AB|=2|AG|=$\sqrt{30}$;…(6分)
(2)设AB的中点为M(x,y),AB的斜率为k,OM⊥AB,
则$\left\{\begin{array}{l}{y-2=k(x+1)}\\{y=-\frac{1}{k}x}\end{array}\right.$,
消去k,得x2+y2-2y+x=0,
当AB的斜率k不存在时也成立,
故过点P的弦的中点的轨迹方程为x2+y2-2y+x=0.…(12分)
点评 本题主要考查了直线与圆的方程的综合运用.解题的过程通过代数的运算解决代数问题,最后翻译成几何结论.

练习册系列答案
相关题目
20.若f(x)=x2-2x-4lnx,则f′(x)<0的解集( )
| A. | (0,+∞) | B. | (0,2) | C. | (0,2)∪(-∞,-1) | D. | (2,+∞) |
17.原点关于x-2y+1=0的对称点的坐标为( )
| A. | ($\frac{4}{5}$,-$\frac{2}{5}$) | B. | (-$\frac{2}{5}$,$\frac{4}{5}$) | C. | ($\frac{4}{5}$,$\frac{2}{5}$) | D. | ($\frac{2}{5}$,-$\frac{4}{5}$) |
4.在△ABC中,内角A,B,C的对边分别是a,b,c,若bcosC=(2a-c)cosB,则B=( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
20.下列结论正确的是( )
| A. | sinx<x,x∈(-π,π) | B. | x-x2>0,x∈(0,2) | C. | ex>1+x,x∈R | D. | lnx≤x-1,x∈(0,+∞) |
16.在△ABC中,$b=\frac{{4\sqrt{3}}}{3}$,c=2$\sqrt{2}$,C=60°,则A等于( )
| A. | 150° | B. | 75° | C. | 105° | D. | 75°或105° |