题目内容
8．过点A（1，2），且平行于向量$\overrightarrow{n}$=（2，1）的直线方程为（ ）| A． | x-2y-3=0 | B． | x-2y+3=0 | C． | 2x-y+3=0 | D． | 以上都不正确 |
分析 通过向量求出直线的斜率，利用点斜式方程求出最新的方程即可．
解答 解：过点A（1，2），且平行于向量$\overrightarrow{n}$=（2，1）的直线方程的斜率为$\frac{1}{2}$，
所以所求直线的方程为：y-2=$\frac{1}{2}$（x-1），即：x-2y+3=0．
故选：B．
点评 本题是基础题，考查直线方程的求法，注意直线的方向向量与直线的斜率的关系，考查计算能力．
练习册系列答案
相关题目
3．已知圆的方程为（x-2）2+（y+3）2=9，则其圆心坐标和半径分别为（ ）
| A． | （2，-3），3 | B． | （-2，3），3 | C． | （3，-2），3 | D． | （-3，2），3 |
13．中心在原点，实轴长为4$\sqrt{3}$，离心率为e=$\sqrt{3}$，焦点在y轴上的双曲线的标准方程是（ ）
| A． | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{36}$=1 | B． | $\frac{{y}^{2}}{12}$-$\frac{{y}^{2}}{36}$=1 | C． | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D． | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 |
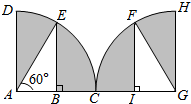如图所示，两个四分之一圆面ACD和GCH交于点C点，AD=CH=10厘米，∠EAB=∠FGC=60°，EB与FI分别垂直于AC和GC，则阴影部分为85.28平方厘米．（π取3.14）