题目内容
18.$\frac{\sqrt{3}tan1{2°-3}^{\;}}{(4co{s}^{2}12°-2)sin12°}$=-4$\sqrt{3}$.分析 先化切为弦,再利用二倍角公式和三角函数恒等式进行等价转化,由此能求出结果.
解答 解:$\frac{\sqrt{3}tan1{2°-3}^{\;}}{(4co{s}^{2}12°-2)sin12°}$
=$\frac{\frac{\sqrt{3}sin12°}{cos12°}-3}{2(2co{s}^{2}12°-1)sin12°}$
=$\frac{\frac{2\sqrt{3}(\frac{1}{2}sin12°-\frac{\sqrt{3}}{2}cos12°)}{cos12°}}{2cos24°sin12°}$
=$\frac{2\sqrt{3}sin(-48°)}{2cos24°sin12°cos12°}$
=$\frac{-2\sqrt{3}sin48°}{sin24°cos24°}$
=$\frac{-2\sqrt{3}sin48°}{\frac{1}{2}sin48°}$
=-4$\sqrt{3}$.
故答案为:-4$\sqrt{3}$.
点评 本题考查三角函数化简求值,是中档题,解题时要认真审题,注意化切为弦、二倍角公式和三角函数恒等式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
13.点P(x,y)满足平面区域:$\left\{\begin{array}{l}{cosθ≤x≤3cosθ}\\{sinθ≤y≤3sinθ}\end{array}\right.$(θ∈R),点M(x,y)满足:(x+5)2+(y+5)2=1,则|$\overrightarrow{PM}$|的最小值是( )
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{2}$-1 | C. | 6$\sqrt{2}$-1 | D. | $\sqrt{61}$-1 |
3.下列各角中,和-40°终边相同的角是( )
| A. | 360° | B. | -320° | C. | 400° | D. | 320° |
8.过点A(1,2),且平行于向量$\overrightarrow{n}$=(2,1)的直线方程为( )
| A. | x-2y-3=0 | B. | x-2y+3=0 | C. | 2x-y+3=0 | D. | 以上都不正确 |
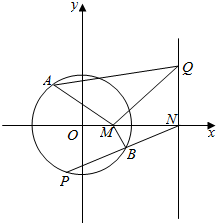 如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).
如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).