题目内容
设等差数列{an}的前n项和为Sn,公比是正数的等比数列{bn}的前n项和为Tn,已知a1=1,b1=3,a2+b2=8,T3-S3=15.
(1)求{an},{bn}的通项公式;
(2)若数列{cn}满足a1cn+a2cn-1+…+an-1c2+anc1=2n+1-n-2对任意n∈N*都成立,求证:数列{cn}是等比数列.
(1)解 设数列{an}的公差为d,数列{bn}的公比为q(q>0).
 (2)证明 由cn+2cn-1+…+(n-1)c2+nc1=2n+1-n-2,
(2)证明 由cn+2cn-1+…+(n-1)c2+nc1=2n+1-n-2,
知cn-1+2cn-2+…+(n-2)c2+(n-1)c1=2n-(n-1)-2(n≥2).
两式相减:cn+cn-1+…+c2+c1=2n-1(n≥2),
∴cn-1+cn-2+…+c2+c1=2n-1-1(n≥3),
∴cn=2n-1(n≥3).
当n=1,2时,c1=1,c2=2,适合上式.
∴cn=2n-1(n∈N*),
即{cn}是等比数列.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 +4
+4 +8=0上的动点,PA、PB是圆
+8=0上的动点,PA、PB是圆 =0的两切线,
=0的两切线, ≥2的解为( )
≥2的解为( ) <0的解集为M.
<0的解集为M.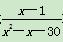 >0的解集是
>0的解集是 )+2的图象向右平移
)+2的图象向右平移 个单位后与原图象重合,则ω的最小值是( )
个单位后与原图象重合,则ω的最小值是( ) B.
B. C.
C. D.3
D.3