Question

2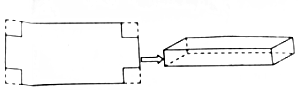．如图，在一张长为2a米，宽为a米（a＞2）的矩形铁皮的四个角上，各剪去一个边长是x米（0＜x≤1）的小正方形，折成一个无盖的长方体铁盒，设V（x）表示铁盒的容积．
（1）试写出V（x）的解析式；
（2）记y=$\frac{V（x）}{x}$，当x为何值时，y最小？并求出最小值．

Answer 1

分析 （1）利用小反弹的体积公式，写出V（x）的解析式；
（2）记y=$\frac{V（x）}{x}$，利用配方法，即可得到当x为何值时，y最小，并求出最小值．

解答 解：（1）由题意，V（x）=（2a-2x）（a-2x）x（0＜x≤1）；
（2）y=$\frac{V（x）}{x}$=（2a-2x）（a-2x）=$4（x-\frac{3}{4}a）^{2}-\frac{1}{4}{a}^{2}$，
∵a＞2，0＜x≤1，∴x=1时，y最小，最小值为2（a-1）（a-2）．

点评 本题考查利用数学知识解决实际问题，考查配方法的运用，属于中档题．