题目内容
平面内两定点M(0,-2)和N(0,2),动点P(x,y)满足|
|•|
|=m(m≥4),动点P的轨迹为曲线E,给出以下五个命题:
①存在m,使曲线E过坐标原点;
②对于任意m,曲线E与x轴有三个交点;
③曲线E关于y轴对称,但不关于x轴对称;
④若P、M、N三点不共线,则△PMN周长的最小值为2
+4;
⑤曲线E上与M、N不共线的任意一点G关于原点对称的点为H,则四边形GMHN的面积不大于m.
其中真命题的序号是 (填上所有正确命题的序号).
| PM |
| PN |
①存在m,使曲线E过坐标原点;
②对于任意m,曲线E与x轴有三个交点;
③曲线E关于y轴对称,但不关于x轴对称;
④若P、M、N三点不共线,则△PMN周长的最小值为2
| m |
⑤曲线E上与M、N不共线的任意一点G关于原点对称的点为H,则四边形GMHN的面积不大于m.
其中真命题的序号是
考点:命题的真假判断与应用,轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用平面内两定点M(0,-2)和N(0,2),动点P(x,y)满足|
|•|
|=m(m≥4),可得
•
=m,对选项进行分析,即可得出结论.
| PM |
| PN |
| x2+(y+2)2 |
| x2+(y-2)2 |
解答:
解:∵平面内两定点M(0,-2)和N(0,2),动点P(x,y)满足|
|•|
|=m(m≥4),
∴
•
=m
①(0,0)代入,可得m=4,∴①正确;
②令y=0,可得x2+4=m,∴对于任意m,曲线E与x轴有三个交点,不正确;
③曲线E关于x轴对称,但不关于y轴对称,故不正确;
④若P、M、N三点不共线,|
|+|
|≥2
=2
,所以△PMN周长的最小值为2
+4,正确;
⑤曲线E上与M、N不共线的任意一点G关于原点对称的点为H,则四边形GMHN的面积为2S△MNG=|GM||GN|sin∠MGN≤m,∴四边形GMHN的面积最大为不大于m,正确.
故答案为:①④⑤.
| PM |
| PN |
∴
| x2+(y+2)2 |
| x2+(y-2)2 |
①(0,0)代入,可得m=4,∴①正确;
②令y=0,可得x2+4=m,∴对于任意m,曲线E与x轴有三个交点,不正确;
③曲线E关于x轴对称,但不关于y轴对称,故不正确;
④若P、M、N三点不共线,|
| PM |
| PN |
|
|
| m |
| m |
⑤曲线E上与M、N不共线的任意一点G关于原点对称的点为H,则四边形GMHN的面积为2S△MNG=|GM||GN|sin∠MGN≤m,∴四边形GMHN的面积最大为不大于m,正确.
故答案为:①④⑤.
点评:本题考查轨迹方程,考查命题的真假判断,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
执行如图程序框图,如果输入的依次为3,5,3,5,5,4,4,3,4,4,则输出的s为( )

A、
| ||||
| B、4 | ||||
C、
| ||||
D、
|
已知sinα<0,cosα<0,则角α是( )
| A、第一象限的角 |
| B、第二象限的角 |
| C、第三象限的角 |
| D、第四象限的角 |
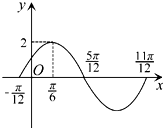 函数y=2sin(ωx+φ)(ω>0,|φ|<
函数y=2sin(ωx+φ)(ω>0,|φ|< 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个三棱锥的表面积为
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个三棱锥的表面积为