题目内容
1．下列说法中错误的是（ ）| A． | 零向量平行于任何向量 | |
| B． | 对于平面上意三点A，B，C，一定有$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | |
| C． | 若$\overrightarrow{AB}$=m$\overrightarrow{CD}$（m∈R），则$\overrightarrow{AB}$∥$\overrightarrow{CD}$ | |
| D． | 若$\overrightarrow{a}$=m$\overrightarrow{i}$，$\overrightarrow{b}$=n$\overrightarrow{j}$，则当m=n时，$\overrightarrow{a}=\overrightarrow{b}$ |
分析 根据向量的定义判断．
解答 解：∵零向量的方向是任意的，故零向量平行于任何向量；A正确．
由向量的三角形法则可知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$．故B正确．
根据平行向量的定义可知C正确．
只有当$\overrightarrow{i}$=$\overrightarrow{j}$，m=n时，才有$\overrightarrow{a}=\overrightarrow{b}$．故D错误．
故选D．
点评 本题考查了平面向量的定义，几何意义，属于基础题．
练习册系列答案
相关题目
11．
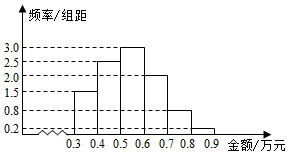某电子商务公司随机抽取l000名网络购物者进行调查，这1000名购物者2015年网上购物金额（单位：万元）均在区间[0.3，0.9]内，样本分组为：[0.3，0.4），[0.4，0.5），
[0.5，0.6），[0.6，0.7），[0.7，0.8），[0.8，0.9]，购物金额的频率分布直方图如下：电子商务公司决定给购物者发放优惠券，其金额（单位：元）与购物金额关系如下：
（I）求这1000名购物者获得优惠券金额的平均数；
（Ⅱ）以这1000名购物者购物金额落在相应区间的频率作为概率，求一个购物者获得优惠券金额不少于150元的概率．
某电子商务公司随机抽取l000名网络购物者进行调查，这1000名购物者2015年网上购物金额（单位：万元）均在区间[0.3，0.9]内，样本分组为：[0.3，0.4），[0.4，0.5），[0.5，0.6），[0.6，0.7），[0.7，0.8），[0.8，0.9]，购物金额的频率分布直方图如下：电子商务公司决定给购物者发放优惠券，其金额（单位：元）与购物金额关系如下：
| 购物金额分组 | [0.3，0.5） | [0.5，0.6） | [0.6，0.8） | [0.8，0.9] |
| 发放金额 | 50 | 100 | 150 | 200 |
（Ⅱ）以这1000名购物者购物金额落在相应区间的频率作为概率，求一个购物者获得优惠券金额不少于150元的概率．