题目内容
15. 如图是函数f(x)=x2+ax-b的部分图象,函数g(x)=ex-f′(x)的零点所在的区间是(k,k+1)(k∈Z),则k的值为( )
如图是函数f(x)=x2+ax-b的部分图象,函数g(x)=ex-f′(x)的零点所在的区间是(k,k+1)(k∈Z),则k的值为( )| A. | -1或0 | B. | 0 | C. | -1或1 | D. | 0或1 |
分析 由f(x)=x2+ax-b的图象可得1<a=1-b<2,求导f′(x)=2x+a,从而化简g(x)=ex-f′(x)=ex-2x-a,求导g′(x)=ex-2,从而确定g(x)的单调性,再利用零点的判定定理解得.
解答 解:∵f(x)=x2+ax-b的图象过点(-1,0),
∴1-a-b=0;即a=1-b;
∵0<f(0)<1,
∴0<-b<1,即-1<b<0,
∴1<a=1-b<2,
而f′(x)=2x+a,
故g(x)=ex-f′(x)=ex-2x-a,
∵g′(x)=ex-2,
∴g(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增;
而g(ln2)=2-2ln2-a<0,
g(-1)=$\frac{1}{e}$+2-a>0,g(0)=1-a<0,
故g(x)在区间(-1,0)上有零点;
g(1)=e-2-a<0,g(2)=e2-4-a>0,
故g(x)在区间(1,2)上有零点;
结合所述,k的值为-1或1;
故选C.
点评 本题考查了数形结合的思想应用及导数的综合应用,同时考查了零点的判定定理的基本应用.

练习册系列答案
相关题目
20.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+x,则f(-2)等于( )
| A. | -2 | B. | 2 | C. | -4 | D. | -6 |
7.椭圆$\frac{x^2}{5}+\frac{y^2}{3}=1$的离心率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
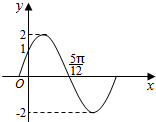 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).