题目内容
7.椭圆$\frac{x^2}{5}+\frac{y^2}{3}=1$的离心率是( )| A. | $\frac{2}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 利用椭圆离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$公式及其椭圆的标准方程即可得出.
解答 解:由椭圆$\frac{x^2}{5}+\frac{y^2}{3}=1$可得:a2=5,b2=3.
可得离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1-\frac{3}{5}}$=$\frac{\sqrt{10}}{5}$.
故选:B.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
15. 如图是函数f(x)=x2+ax-b的部分图象,函数g(x)=ex-f′(x)的零点所在的区间是(k,k+1)(k∈Z),则k的值为( )
如图是函数f(x)=x2+ax-b的部分图象,函数g(x)=ex-f′(x)的零点所在的区间是(k,k+1)(k∈Z),则k的值为( )
 如图是函数f(x)=x2+ax-b的部分图象,函数g(x)=ex-f′(x)的零点所在的区间是(k,k+1)(k∈Z),则k的值为( )
如图是函数f(x)=x2+ax-b的部分图象,函数g(x)=ex-f′(x)的零点所在的区间是(k,k+1)(k∈Z),则k的值为( )| A. | -1或0 | B. | 0 | C. | -1或1 | D. | 0或1 |
2.若将f(x)=2sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位,再将纵坐标不变,横坐标变为原来的$\frac{1}{2}$,得g(x)的图象,且g(x)图象关于直线x=-$\frac{π}{12}$对称,则f($\frac{π}{4}$)=( )
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
19.过两点(2,5),(2,-5)的直线方程是( )
| A. | x=5 | B. | y=2 | C. | x+y=2 | D. | x=2 |
16.一个正方体内接于高为$\sqrt{2}$m,底面半径为1m的圆锥中,则正方体的棱长是( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
17.如图所示是一个几何体的三视图,则这个几何体的表面积为( )
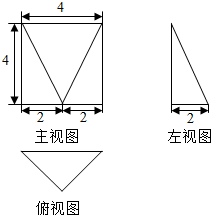

| A. | $20+4\sqrt{2}+4\sqrt{5}$ | B. | $20+8\sqrt{2}$ | C. | $20+8\sqrt{2}+4\sqrt{5}$ | D. | $20+4\sqrt{5}$ |