题目内容
已知函数m(x)=x3-
x2,h(x)=
ax2-3ax
(1)若函数f(x)=m(x)-h(x)在x=1处取得极值,求实数a的值;
(2)若函数f(x)=m(x)-h(x)在(-∞,+∞)不单调,求实数a的取值范围;
(3)判断过点A(1,-
)可作曲线f(x)=m(x)+
x2-3x多少条切线,并说明理由.
| 3 |
| 3 |
(1)若函数f(x)=m(x)-h(x)在x=1处取得极值,求实数a的值;
(2)若函数f(x)=m(x)-h(x)在(-∞,+∞)不单调,求实数a的取值范围;
(3)判断过点A(1,-
| 5 |
| 2 |
| 3 |
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:计算题,函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(1)求出函数f(x)的导数,由条件得,f′(1)=0求得a,注意检验x=1处导数的符号;
(2)若函数f(x)在R上不单调,则f′(x)=3x2-2
(a+1)x+3a=0应有二不等根,则△=12(a+1)2-36a>0,解出a即可;
(3)求出导数,设出切点,求出切线的斜率,再由两点的斜率公式,得到方程,构造函数g(x0)=2x03-3x02+
,运用导数求出极值,令极大值大于0,极小值小于0,即可判断函数有三个零点,即方程有三个实根,即切线有三条.
(2)若函数f(x)在R上不单调,则f′(x)=3x2-2
| 3 |
(3)求出导数,设出切点,求出切线的斜率,再由两点的斜率公式,得到方程,构造函数g(x0)=2x03-3x02+
| 1 |
| 2 |
解答:
解:(1)∵函数m(x)=x3-
x2,h(x)=
ax2-3ax,
∴f(x)=m(x)-h(x)=x3-
(1+a)x2+3ax,
∴f′(x)=3x2-2
(a+1)x+3a,
∵f′(1)=0,∴3+3a-2
(a+1)=0∴a=-1,
∴f′(x)=3(x-1)(x+1),显然在x=1附近f′(x)符号不同,
∴x=1是函数f(x)的一个极值点,
∴a=-1即为所求;
(2)∵m(x)=x3-
x2,h(x)=
ax2-3ax,
∴∴f(x)=m(x)-h(x)=x3-
(1+a)x2+3ax,
若函数f(x)在R上不单调,
则f′(x)=3x2-2
(a+1)x+3a=0应有二不等根,
∴△=12(a+1)2-36a>0∴a2-a+1>0恒成立,
∴实数a的取值范围为R;
(3)∵m(x)=x3-
x2,∴f(x)=m(x)+
x2-3x=x3-3x,
∴f'(x)=3(x2-1),设切点M(x0,y0),
则M的纵坐标y0=x03-3x0,又f′(x0)=3(x02-1),
∴切线的斜率为3(x02-1)=
,得2x03-3x02+
=0,
设g(x0)=2x03-3x02+
,∴g'(x0)=6x02-6x0
由g'(x0)=0,得x0=0或x0=1,
∴g(x0)在(-∞,0),(1,+∞)上为增函数,在(0,1)上为减函数,
∴函数g(x0)=2x03-3x02+m+3的极大值点为x0=0,极小值点为x0=1,
∵
∴函数g(x0)=2x03-3x02+
有三个零点,
∴方程2x03-3x02+
=0有三个实根,
∴过点A(1,-
)可作曲线y=f(x)的三条切线.
| 3 |
| 3 |
∴f(x)=m(x)-h(x)=x3-
| 3 |
∴f′(x)=3x2-2
| 3 |
∵f′(1)=0,∴3+3a-2
| 3 |
∴f′(x)=3(x-1)(x+1),显然在x=1附近f′(x)符号不同,
∴x=1是函数f(x)的一个极值点,
∴a=-1即为所求;
(2)∵m(x)=x3-
| 3 |
| 3 |
∴∴f(x)=m(x)-h(x)=x3-
| 3 |
若函数f(x)在R上不单调,
则f′(x)=3x2-2
| 3 |
∴△=12(a+1)2-36a>0∴a2-a+1>0恒成立,
∴实数a的取值范围为R;
(3)∵m(x)=x3-
| 3 |
| 3 |
∴f'(x)=3(x2-1),设切点M(x0,y0),
则M的纵坐标y0=x03-3x0,又f′(x0)=3(x02-1),
∴切线的斜率为3(x02-1)=
x03-3x0+
| ||
| x0-1 |
| 1 |
| 2 |
设g(x0)=2x03-3x02+
| 1 |
| 2 |
由g'(x0)=0,得x0=0或x0=1,
∴g(x0)在(-∞,0),(1,+∞)上为增函数,在(0,1)上为减函数,
∴函数g(x0)=2x03-3x02+m+3的极大值点为x0=0,极小值点为x0=1,
∵
|
| 1 |
| 2 |
∴方程2x03-3x02+
| 1 |
| 2 |
∴过点A(1,-
| 5 |
| 2 |
点评:本题考查导数的综合应用:求切线方程和求单调区间和求极值,考查函数的零点和方程根的关系,以及运用导数求得极值的符号与零点的关系,考查运算能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
下列各图中,不可能表示函数y=f(x)的图象的是( )
A、 |
B、 |
C、 |
D、 |
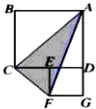 如图,点E在正方形ABCD边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a,b为常数,且a>b>0),则△ACF的面积( )
如图,点E在正方形ABCD边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a,b为常数,且a>b>0),则△ACF的面积( )| A、只与a的大小有关 |
| B、只与b的大小有关 |
| C、只与CE的大小有关 |
| D、无法确定 |
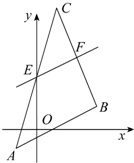 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的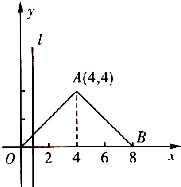 如图所示,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为(x,0).
如图所示,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为(x,0).