题目内容
| 2sin100°-cos70° |
| cos20° |
| A、4 | ||
B、2
| ||
| C、2 | ||
D、
|
考点:三角函数的化简求值
专题:三角函数的求值
分析:利用两角差的余弦与诱导公式即可将所求关系式化简并求得其值.
解答:
解:原式=
=
=
=2cos30°=
.
故选:D.
| 2cos10°-sin20° |
| cos20° |
| 2(cos30°-20°)-sin20° |
| cos20° |
| 2cos30°cos20°+2sin30°sin20°-sin20° |
| cos20° |
| 3 |
故选:D.
点评:本题考查三角函数的化简求值,考查两角差的余弦与诱导公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x-2x+b(b为常数),则f(-1)=( )
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
若函数h(x)在定义域D上可导,且其导函数h′(x)在D上也可导,则称h(x)在D上存在二阶导函数,记作h″(x),即h″(x)=(h′(x))′,当h″(x)<0在D上恒成立时,称h(x)在D上是凸函数.下列函数在(0,
)上不是凸函数的是( )
| π |
| 2 |
| A、f(x)=sinx+cosx+m(m∈R) |
| B、f(x)=lnx-2015x+m(m∈R) |
| C、f(x)=-x3+2020x+m(m∈R) |
| D、f(x)=xex+m(m∈R) |
已知集合A={-1,0},B={0,1},则集合∁A∪B(A∩B)( )
| A、φ | B、{0} |
| C、{-1,1} | D、{-1,0,1} |
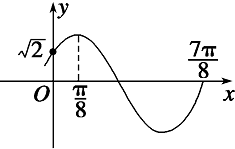 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<