题目内容
已知函数y=f(x)满足f(x+y)=f(x)+f(y)对任何实数x,y都成立.
(1)求证:f(2x)=2f(x);
(2)求f(0)的值;
(3)求证f(x)为奇函数.
(1)求证:f(2x)=2f(x);
(2)求f(0)的值;
(3)求证f(x)为奇函数.
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:(1)依题意,令y=x,即可证得f(2x)=2f(x);
(2)令y=x=0,即可求得f(0)=0;
(3)令y=-x,可证得f(-x)=-f(x),从而可证f(x)为奇函数.
(2)令y=x=0,即可求得f(0)=0;
(3)令y=-x,可证得f(-x)=-f(x),从而可证f(x)为奇函数.
解答:
证明:(1)∵(x+y)=f(x)+f(y),
令y=x,得f(x+x)=f(x)+f(x),即f(2x)=2f(x);
(2)令y=x=0,
∵f(x+y)=f(x)+f(y),
∴f(0+0)=f(0)+f(0),即f(0)=2f(0),
∴f(0)=0.
(3)证明:由已知得定义域为R.满足若x∈R,则-x∈R.
令y=-x,
∵f(x+y)=f(x)+f(y),
∴f(0)=f(x)+f(-x).
∵f(0)=0,
∴f(x)+f(-x)=0,即f(-x)=-f(x).
∴f(x)为奇函数.
令y=x,得f(x+x)=f(x)+f(x),即f(2x)=2f(x);
(2)令y=x=0,
∵f(x+y)=f(x)+f(y),
∴f(0+0)=f(0)+f(0),即f(0)=2f(0),
∴f(0)=0.
(3)证明:由已知得定义域为R.满足若x∈R,则-x∈R.
令y=-x,
∵f(x+y)=f(x)+f(y),
∴f(0)=f(x)+f(-x).
∵f(0)=0,
∴f(x)+f(-x)=0,即f(-x)=-f(x).
∴f(x)为奇函数.
点评:本题考查抽象函数及其应用,着重考查赋值法的应用,考查函数的奇偶性的判定,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
曲线y=
在点(0,0)处的切线方程为( )
| x |
| x+1 |
| A、y=-x | ||
B、y=
| ||
| C、y=x | ||
| D、y=2x |
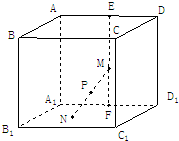 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AD,A1D1的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A1B1C1D1上运动,则线段MN的中点P在二面角A-A1D1-B1内运动所形成的轨迹(曲面)的面积为( )
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AD,A1D1的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A1B1C1D1上运动,则线段MN的中点P在二面角A-A1D1-B1内运动所形成的轨迹(曲面)的面积为( )| A、4π | ||
| B、π | ||
C、
| ||
| D、2π |
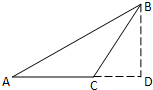 已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若
已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若| AB |
| a |
| AC |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|