题目内容
9.已知{an}是递增的等差数列,a2,a4是方程x2-10x+24=0的根.(1)求{an}的通项公式;
(2)求数列{$\frac{{a}_{n}}{{2}^{n+1}}$}的前n项和.
分析 (1)由韦达定理得a2=4,a4=6,由此能求出{an}的通项公式.
(2)由$\frac{{a}_{n}}{{2}^{n+1}}$=$\frac{n+2}{{2}^{n+1}}$,利用错位相减法能求出数列{$\frac{{a}_{n}}{{2}^{n+1}}$}的前n项和.
解答 解:(1)∵{an}是递增的等差数列,a2,a4是方程x2-10x+24=0的根,
∴a2<a4,解方程x2-10x+24=0,得x1=4,x2=6,
∴a2=4,a4=6,
∴$\left\{\begin{array}{l}{{a}_{1}+d=4}\\{{a}_{1}+3d=6}\end{array}\right.$,解得a1=3,d=1,
∴an=3+(n-1)×1=n+2.
(2)∵$\frac{{a}_{n}}{{2}^{n+1}}$=$\frac{n+2}{{2}^{n+1}}$,
∴数列{$\frac{{a}_{n}}{{2}^{n+1}}$}的前n项和:
Sn=$\frac{3}{{2}^{2}}+\frac{4}{{2}^{3}}+\frac{5}{{2}^{4}}+…+\frac{n+2}{{2}^{n+1}}$,①
$\frac{1}{2}{S}_{n}$=$\frac{3}{{2}^{3}}+\frac{4}{{2}^{4}}+\frac{5}{{2}^{5}}+…+\frac{n+2}{{2}^{n+2}}$,②
①-②,得:$\frac{1}{2}{S}_{n}$=$\frac{3}{4}$+$\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}+\frac{1}{{2}^{5}}+…+\frac{1}{{2}^{n+1}}$-$\frac{n+2}{{2}^{n+2}}$
=$\frac{3}{4}$+$\frac{\frac{1}{8}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-$\frac{n+2}{{2}^{n+2}}$
=1-$\frac{1}{{2}^{n+1}}-\frac{n+2}{{2}^{n+2}}$,
∴Sn=2-$\frac{n+4}{{2}^{n+1}}$.
点评 本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案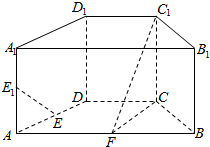 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.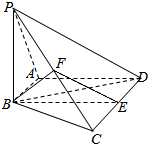 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.