题目内容
20.判断下列函数的奇偶性:(1)f(x)=$\sqrt{{x}^{2}-1}$+$\sqrt{1-{x}^{2}}$
(2)f(x)=|x+1|-|x-1|
(3)f(x)=$\left\{\begin{array}{l}{-{x}^{2}+x(x>0)}\\{{x}^{2}+x(x≤0)}\end{array}\right.$
(4)f(x)=x2lg(x+$\sqrt{{x}^{2}+1}$)
分析 根据函数奇偶性的定义进行判断即可.
解答 解:(1)要使函数有意义,则$\left\{\begin{array}{l}{{x}^{2}-1≥0}\\{1-{x}^{2}≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{x^2≥1}\\{x^2≤1}\end{array}\right.$
解得x2=1,即x=±1,定义域关于原点对称,
则f(-x)=$\sqrt{{x^2}-1}$+$\sqrt{1-{x^2}}$=f(x).且f(1)=f(-1)=0,
故函数f(x)是既是奇函数也是偶函数.
(2)f(-x)=|-x+1|-|-x-1|=|x-1|-|x+1|=-f(x),
则f(x)是奇函数;
(3)若x>0,则-x<0,则f(-x)=x2-x=-(x2+x)=-f(x),
若x<0,则-x>0,则f(-x)=-x2-x=-(x2+x)=-f(x),
综上f(-x)=-f(x),则f(x)是奇函数;
(4)f(-x)=x2lg(-x+$\sqrt{{x}^{2}+1}$)=x2lg$\frac{(\sqrt{{x}^{2}+1}-x)(\sqrt{{x}^{2}+1}+x)}{\sqrt{{x}^{2}+1}+x}$=x2lg$\frac{1}{\sqrt{{x}^{2}+1}+x}$=-x2lg(x+$\sqrt{{x}^{2}+1}$)=-f(x),
则f(x)是奇函数.
点评 本题主要考查函数奇偶性的应用,利用函数奇偶性的定义是解决本题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
8.若$\frac{sinα}{\sqrt{1-co{s}^{2}α}}$=$\frac{cosα}{\sqrt{1-si{n}^{2}α}}$,则角α是( )
| A. | 第一象限 | B. | 第三象限 | ||
| C. | 第一象限或第三象限 | D. | 第二象限或第四象限 |
5.方程x2+y2+x+2y+a-1=0表示圆,则a的取值范围是( )
| A. | (-∞,-2) | B. | (-$\frac{2}{3}$,0) | C. | ($\frac{9}{4}$,+∞) | D. | (-∞,$\frac{9}{4}$) |
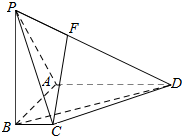 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.