题目内容
命题p：?x∈Z，则x2-4＞0；与命题q：?x∈Z，使x2-4＞0，下列结论正确的是（ ）
| A、p真q假 | B、p假q真 |
| C、p∧q为真 | D、p∨q为假 |
考点：复合命题的真假
专题：简易逻辑
分析：先判断命题p与q的真假，再利用复合命题真假的判定方法即可得出．
解答：
解：命题p：?x∈Z，则x2-4＞0，是假命题，例如取x=0，则不成立；
命题q：?x∈Z，使x2-4＞0，是真命题，例如取x=3．
∴p假q真．
故选：B．
命题q：?x∈Z，使x2-4＞0，是真命题，例如取x=3．
∴p假q真．
故选：B．
点评：本题考查了简易逻辑的判定方法，考查了推理能力，属于基础题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
函数f（x）=
的递增区间为（ ）
| x2-4x |
| A、[2，+∞） |
| B、[4，+∞） |
| C、（-∞，2] |
| D、（-∞，4] |
在一个△ABC中，若a=2，b=2，A=30°，那么B等于（ ）
| A、60° |
| B、60°或 120° |
| C、30° |
| D、30°或150° |
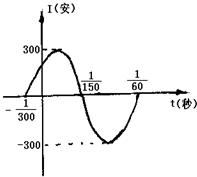如图，表示电流强度I与时间t的关系式I=Asin（ωt+φ）（A＞0，ω＞0），在一个周期内的图象．
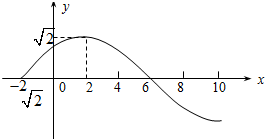已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜若a=sin（cosπx），b=cos（sinπx）且x∈[-
，-1]，则（ ）
| 3 |
| 2 |
| A、a2+b2=1 |
| B、a＜b |
| C、a＞b |
| D、a=b |