题目内容
如图，弦AD和CE相较于⊙O内一点F，延长EC与过点A的切线相交于点B，已知AB=BF=FD，BC=1，CE=8，求AB及AF的长．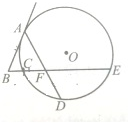
考点：与圆有关的比例线段
专题：直线与圆
分析：由切割线定理得AB2=BC•BE=BC（BC+CE），由此能求出AB=3，从而BF=DF=3，进而EF=BE-BF=6，CF=BF-BC=2，由相交弦定理，得，AF•DF=CF•EF，由此能求出AF．
解答：
解：∵AB是切线，BCE是割线，BC=1，CE=8，
∴AB2=BC•BE=BC（BC+CE）=1×9=9，
解得AB=3，
∴BF=DF=3，
∴EF=BE-BF=9-3=6，CF=BF-BC=3-1=2，
在圆中，由相交弦定理，得，AF•DF=CF•EF，
即3•AF=2×6=12，
解得AF=4．
∴AB2=BC•BE=BC（BC+CE）=1×9=9，
解得AB=3，
∴BF=DF=3，
∴EF=BE-BF=9-3=6，CF=BF-BC=3-1=2，
在圆中，由相交弦定理，得，AF•DF=CF•EF，
即3•AF=2×6=12，
解得AF=4．
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意切割线定理和相交弦定理的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
下列说法正确的是（ ）
| A、命题“若x=2，则x2=4”的否命题为“若x2≠4，则x≠2” |
| B、命题“?x∈R，x2+x-1＜0”的否定是“?x∈R，x2+x-1＞0” |
| C、“x=y”是“sinx=siny”的充分不必要条件 |
| D、命题“若x=0或y=0，则xy=0”的逆否命题为“若xy≠0，则x≠0或y≠0” |
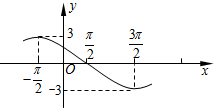已知函数f（x）=Acos（ωx+φ） （A＞0，ω＞0，|φ|＜
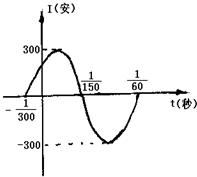如图，表示电流强度I与时间t的关系式I=Asin（ωt+φ）（A＞0，ω＞0），在一个周期内的图象．