题目内容
已知数列{an}的前n项和Sn,满足Sn=a(Sn-an+1)(a为常数,且a>0),且4a3是a1与2a2的等差中项.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=(2n+1)an,求数列{bn}的前n项和Tn.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=(2n+1)an,求数列{bn}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知得S1=a1=a(a1-a1+1),Sn-1=a(Sn-1-an-1+1),从而{an}是首项为a公比为a的等比数列,进而an=a•an-1=an.由4a3是a1与2a2的等差中项,得8a3=a+2a2,由此能求出an=(
)n.
(Ⅱ)由bn=(2n+1)an=(2n+1)•(
)n,利用错位相减法能求出Tn=5-(2n+5)(
)n.
| 1 |
| 2 |
(Ⅱ)由bn=(2n+1)an=(2n+1)•(
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)∵Sn=a(Sn-an+1),
∴S1=a1=a(a1-a1+1),解得a1=1,
当n≥2时,Sn=a(Sn-an+1),Sn-1=a(Sn-1-an-1+1),
两式相减,得an=a•an-1,∴
=a,
∴{an}是首项为a公比为a的等比数列,
∴an=a•an-1=an.
∵4a3是a1与2a2的等差中项,
∴8a3=a1+2a2,即8a3=a+2a2,
解得a=
,或a=0(舍),或a=-
(舍),
∴an=(
)n.
(Ⅱ)∵bn=(2n+1)an=(2n+1)•(
)n,
∴Tn=3×
+5×(
)2+7×(
)3+…+(2n+1)•(
)n,①
Tn=3×(
)2+5×(
)3+7×(
)4+…+(2n+1)×(
)n+1,②
①-②得:
Tn=
+2×[(
)2+(
)3+…+(
)n]-(2n+1)×(
)n+1
=
+2×
-(2n+1)×(
)n+1
=
-(2n+5)(
)n+1,
∴Tn=5-(2n+5)(
)n.
∴S1=a1=a(a1-a1+1),解得a1=1,
当n≥2时,Sn=a(Sn-an+1),Sn-1=a(Sn-1-an-1+1),
两式相减,得an=a•an-1,∴
| an |
| an-1 |
∴{an}是首项为a公比为a的等比数列,
∴an=a•an-1=an.
∵4a3是a1与2a2的等差中项,
∴8a3=a1+2a2,即8a3=a+2a2,
解得a=
| 1 |
| 2 |
| 1 |
| 4 |
∴an=(
| 1 |
| 2 |
(Ⅱ)∵bn=(2n+1)an=(2n+1)•(
| 1 |
| 2 |
∴Tn=3×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得:
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
=
| 5 |
| 2 |
| 1 |
| 2 |
∴Tn=5-(2n+5)(
| 1 |
| 2 |
点评:本题主要考查数列的通项公式、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想,解题时要注意错位相减法的合理运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
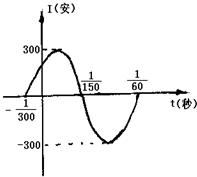 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.