Question

ABCD为直角梯形，∠DAB=∠ABC=90°，AB=BC=a，AD=2a，PA⊥平面ABCD，PA=a，
（1）求证：PC⊥CD；
（2）求点B到直线PC的距离．

Answer 1

考点：直线与平面垂直的性质

专题：空间位置关系与距离

分析：（1）连结AC，由勾股定理可得AC⊥CD，由线面垂直的性质定理可得：PA⊥CD，进而由线面垂直的判定定理得到CD⊥平面PAC，进而得到PC⊥CD；
（2）由已知可得△PBC为Rt△，∠PBC=90°，进而利用等积法可求得点B到直线PC的距离．

解答： 证明：（1）连结AC，

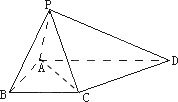
∵∠ABC=90°，AB=BC=a，
由勾股定理得AC=

2

a，
同理CD=

2

a，
又∵AD=2a，
∴△ACD是直角三角形．
即AC⊥CD，
又∵PA⊥平面ABCD，CD?平面ABCD，
∴PA⊥CD，
又∵AC，PA?PAC，AC∩PA=A，
∴CD⊥平面PAC，
又由PC?平面PAC，
∴PC⊥CD．
（2）在Rt△PAB中，PA=AB=a，
∴PB=

2

a，
在Rt△PAC中，AC=

2

a，
∴PC=

3

a，
又∵BC=a，
故△PBC为Rt△，∠PBC=90°，
令点B到直线PC的距离为h，
则

1

2

PC•h=

1

2

PB•BC，
∴h=

PB•BC

PC

=

2 a•a

3 a

=

6

3

a，
即点B到直线PC的距离为

6

3

a．

点评：本题考查的知识点是直线与平面垂直的性质，点到直线的距离，难度不大，属于基础题．