Question

4．已知函数f（x）=-x²+2x，g（x）=$\left\{\begin{array}{l}{f（x）}&{x≤a}\\{g（x-1）-1}&{x＞a}\end{array}\right.$，关于x的方程g（x）=t对于任意的t＜1都恰有两个不同的解，则实数a取值集合是{2}．

Answer 1

分析 通过当x≤a时，求出g（x，当a＜x≤a+1时，得到g（x）在（a，a+1]上的图象，然后分析判断交点个数．

解答 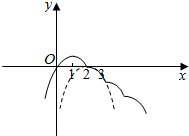解：当x≤a时，g（x）=f（x）=-x²+2x，当a＜x≤a+1时，a-1＜x-1≤a，
g（x-1）=f（x-1），又因为g（x）=g（x-1）-1．所以g（x）=f（x-1）-1，将
y=-x²+2x向右平移1单位，在向下平移1单位，可得y=-（x-2）²，可得g（x）在（a，a+1]上的图象，如图所示，
注意到点（2，0）在y=-x²+2x上，要使?t＜1，g（x）=t只有两解，当a＞2或a＜2时，g（x）=t的解的个数不等于2个，不符合题意，
所以a=2，
又因为g（2）=0，g（3）=-1，所以可以保证在其余的位置当?t＜1时，g（x）=t只有两解．
故答案为：{2}．

点评 本题考查函数的图象的应用，函数的零点个数的判断，考查计算能力．