题目内容
20.已知函数$\begin{array}{l}\\ f(x)={x^2}-2x+2,x∈[{-2,2}]\end{array}$(1)求函数的顶点坐标
(2)求y=f(x)在区间[-2,2]上的最大值和最小值.
分析 (1)将f(x)配方,求出f(x)的顶点坐标;(2)求出函数的对称轴,求出函数的最大值和最小值即可.
解答 解:f(x)=(x-1)2+1,x∈[-2,2],
(1)函数的顶点坐标是(1,1);
(2)f(x)的对称轴是x=1,
故f(x)在[-2,1)递减,在(1,2]递增,
故f(x)的最大值是f(-2)=10,f(x)的最小值是f(1)=1.
点评 本题考查了函数的单调性、最值问题,考查二次函数的性质,是一道基础题.

练习册系列答案
相关题目
10.4个男生4个女生站成一排,要求相邻两人性别不同且男生甲与女生乙相邻,则这样的站法有( )
| A. | 576种 | B. | 504种 | C. | 288种 | D. | 252种 |
11.如图某几何体的三视图是直角边长为1的三个等腰直角三角形,则该几何体的外接球的表面积为( )
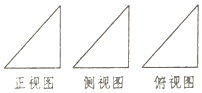

| A. | $\frac{3}{2}π$ | B. | $\sqrt{3}π$ | C. | $\frac{{\sqrt{3}}}{2}π$ | D. | 3π |
8.设全集U={(x,y)|x,y∈R},集合M={(x,y)|$\frac{y-3}{x-2}$=1},N={(x,y)|y=x+1},则N∩(∁UM)等于( )
| A. | ∅ | B. | {(2,3)} | C. | (2,3) | D. | {(x,y)|y=x+1} |
12.下列命题中错误的是( )
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x>5”是“x2-4x-5>0”的充分不必要条件 | |
| C. | 命题p:?x0∈R,x02+x0-1<0,则?p:?x∈R,x2+x-1≥0 | |
| D. | 命题“若x2-3x+2=0,则x=1或x=2”的逆否命题为“若x≠1且x≠2,则x2-3x+2≠0” |
9.函数f(x)=x3+4x+9的图象在x=1处的切线在x轴上的截距为( )
| A. | 7 | B. | 1 | C. | -1 | D. | -7 |