题目内容
13．
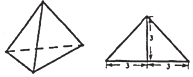已知一个正三棱锥的正视图为等腰直角三角形，其尺寸如图所示，则此正三棱锥的体积9$\sqrt{3}$，其侧视图的周长为$5\sqrt{3}+\sqrt{21}$．
分析 通过三棱锥的正视图的数据，推出正三棱锥的底面边长，三棱锥的高，然后求出三棱锥的斜高，侧棱长，底面上的高，即可求出此正三棱锥的体积、侧视图的周长．
解答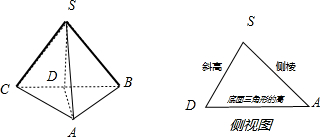 
解：三棱锥的正视图的数据，可知正三棱锥的底面边长为6，三棱锥的高为3，
所以三棱锥的底面上的高为$\sqrt{36-9}$=3$\sqrt{3}$，斜高为$\sqrt{9+3}$=2$\sqrt{3}$，
侧棱长为$\sqrt{9+12}$=$\sqrt{21}$，
所以正三棱锥的体积为$\frac{1}{3}×\frac{\sqrt{3}}{4}×36×3$=9$\sqrt{3}$
侧视图的周长为3$\sqrt{3}$+2$\sqrt{3}$+$\sqrt{21}$=$5\sqrt{3}+\sqrt{21}$．
故答案为9$\sqrt{3}$；$5\sqrt{3}+\sqrt{21}$．
点评 本题考查三视图与直观图的关系，考查空间想象能力，计算能力．
练习册系列答案
相关题目
1．若$\left\{{1，a，\frac{b}{a}}\right\}=\left\{{0，{a^2}，a+b}\right\}$，则a2017+b2017的值为（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 1或-1 |
8．设全集U={（x，y）|x，y∈R}，集合M={（x，y）|$\frac{y-3}{x-2}$=1}，N={（x，y）|y=x+1}，则N∩（∁UM）等于（ ）
| A． | ∅ | B． | {（2，3）} | C． | （2，3） | D． | {（x，y）|y=x+1} |
18．幂函数y=x-1不具有的特性是 （ ）
| A． | 在定义域内是减函数 | B． | 图象过定点（1，1） | ||
| C． | 是奇函数 | D． | 其定义域是R |
2．如图所示的直观图，其表示的平面图形是（ ）
| A． | 正三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 锐角三角形 |