题目内容
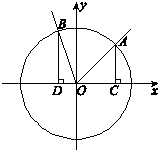
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且α∈(
,
).将角α的终边按逆时针方向旋转
,交单位圆于点B.记A(x1,y1),B(x2,y2).
(Ⅰ)若x1=
,求x2;
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=S2,求角α的值.
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
(Ⅰ)若x1=
| 1 |
| 4 |
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=S2,求角α的值.

(I)由三角函数定义,得x1=cosα,x2=cos(α+
),
∵α∈(
,
),cosα=
,
∴sinα=
=
,
∴x2=cos(α+
)=
cosα-
sinα=
.
(Ⅱ)依题意得y1=sinα,y2=sin(α+
).
∴S1=
x1y1=
sin2α,
S2=
|x2|y2=
sin(α+
)|cos(α+
)|=-
sin(2α+
),
∵S1=S2
∴sin2α=-sin(2α+
)=-
sin2α-
cos2α,
整理得tan2α=-
,
∵
<α<
,
∴
<2α<π,
∴2α=
,即α=
.
| π |
| 6 |
∵α∈(
| π |
| 3 |
| π |
| 2 |
| 1 |
| 4 |
∴sinα=
1-(
|
| ||
| 4 |
∴x2=cos(α+
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 8 |
(Ⅱ)依题意得y1=sinα,y2=sin(α+
| π |
| 6 |
∴S1=
| 1 |
| 2 |
| 1 |
| 4 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 4 |
| π |
| 3 |
∵S1=S2
∴sin2α=-sin(2α+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
整理得tan2α=-
| ||
| 3 |
∵
| π |
| 3 |
| π |
| 2 |
∴
| 2π |
| 3 |
∴2α=
| 5π |
| 6 |
| 5π |
| 12 |

练习册系列答案
相关题目
 ,顶角为
,顶角为 的等腰三角形.
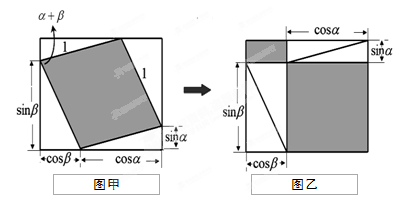
的等腰三角形. 时,求该八边形的面积;
时,求该八边形的面积;  的取值范围,当
的取值范围,当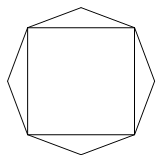
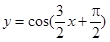 是奇函数;②存在实数
是奇函数;②存在实数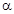 ,使得
,使得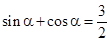 ;③若
;③若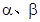 是第一象限角且
是第一象限角且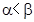 ,则
,则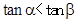 ;④
;④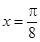 是函数
是函数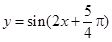 的一条对称轴;⑤
的一条对称轴;⑤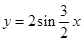 在区间
在区间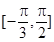 上的最小值是-2,最大值是
上的最小值是-2,最大值是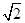 ,其中正确命题的序号是.
,其中正确命题的序号是.