题目内容

在△ABC中的内角A、B、C所对的边分别为a，b，c，若b=2ccosA，c=2bcosA则△ABC的形状为（　　）
A．直角三角形B．锐角三角形
C．等边三角形D．等腰直角三角形
因为在△ABC中的内角A、B、C所对的边分别为a，b，c，若b=2ccosA，c=2bcosA
所以
b
c
=
2ccosA
2bcosA
，所以b=c，2bcosA=c，所以cosA=
1
2
，A=60°，
所以三角形是正三角形．
故选C．
练习册系列答案
相关题目
在△ABC中，角A，B，C所对的边分别为a，b，c，且asinB-bcosC=ccosB．
（Ⅰ）判断△ABC的形状；
（Ⅱ）若f（x）=sinx+cosx，求f（A）的最大值．
已知平面向量
a
=（
2
，
2
），
b
=（sin
π
4
x，cos
π
4
x），函数f（x）=
a
•
b
．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）将函数f（x）的图象上的所有的点向左平移1个单位长度，得到函数y=g（x）的图象，若函数y=g（x）+k在（-2，4）上有两个零点，求实数k的取值范围．
设△ABC的内角A，B，C成等差数列，且满足条件sinAcosC=cos（120°-C）sinC，试判断△ABC的形状，并证明你的结论．
在△ABC中，角A、B、C的大小成等差数列，则sin（A+C）=（　　）
A．-
1
2
B．
3
2
C．-
3
2
D．
1
2
已知函数f(x)=
3
sin2ωx+2cos2ωx(ω＞0)的最小正周期为π．
（I）求ω的值；
（II）求函数f（x）在区间[0，
π
2
]的取值范围．
如图，在直角坐标系xOy中，角α的顶点是原点，始边与x轴正半轴重合，终边交单位圆于点A，且α∈(
π
3
，
π
2
)．将角α的终边按逆时针方向旋转
π
6
，交单位圆于点B．记A（x1，y1），B（x2，y2）．
（Ⅰ）若x1=
1
4
，求x2；
（Ⅱ）分别过A，B作x轴的垂线，垂足依次为C，D．记△AOC的面积为S1，△BOD的面积为S2．若S1=S2，求角α的值．
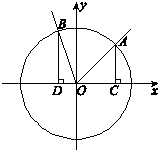
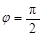“”是“函数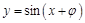的图象关于y轴对称”的
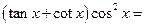   条件．（在“充分必要”、“充分不必要”、“必要不充分”、
“既不充分也不必要”中选一个合适的填空）
(     )
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网