题目内容
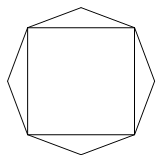
某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为 ,顶角为
,顶角为 的等腰三角形.
的等腰三角形.
(1)若角 时,求该八边形的面积;
时,求该八边形的面积;
(2)写出 的取值范围,当
的取值范围,当 取何值时该八边形的面积最大,并求出最大面积.
取何值时该八边形的面积最大,并求出最大面积.
 ,顶角为
,顶角为 的等腰三角形.
的等腰三角形.(1)若角
 时,求该八边形的面积;
时,求该八边形的面积; (2)写出
 的取值范围,当
的取值范围,当 取何值时该八边形的面积最大,并求出最大面积.
取何值时该八边形的面积最大,并求出最大面积.
(1) ;(2)
;(2) ,当
,当 时,八边形的面积取最大值
时,八边形的面积取最大值 .
.
 ;(2)
;(2) ,当
,当 时,八边形的面积取最大值
时,八边形的面积取最大值 .
.试题分析:(1)先利用
 结合余弦定理确定正方形的边长,然后将八边形分为一个正方形与四个等腰三角形求面积,最后将面积相加得到八边形的面积;(2)利用
结合余弦定理确定正方形的边长,然后将八边形分为一个正方形与四个等腰三角形求面积,最后将面积相加得到八边形的面积;(2)利用 得到角
得到角 的取值范围,利用正弦定理求出正方形的边长(利用含
的取值范围,利用正弦定理求出正方形的边长(利用含 的代数式表示),然后利用面积公式求出八边形的面积关于
的代数式表示),然后利用面积公式求出八边形的面积关于 的三角函数,结合降幂公式、辅助角公式将三角函数解析式进行化简,最后求出相应函数在区间
的三角函数,结合降幂公式、辅助角公式将三角函数解析式进行化简,最后求出相应函数在区间 的最大值.
的最大值.(1)由题可得正方形边长为
 ,
, ;
;(2)显然
 ,所以
,所以 ,
,
 ,
, ,
, ,故
,故 ,
,  ,此时
,此时 .
.
练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
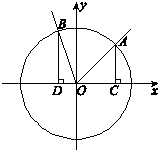
 则
则 .
. ,例如
,例如 ,则
,则 的最大值为( )
的最大值为( )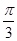 ”是“cos θ≠
”是“cos θ≠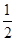 ”的( )
”的( )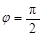 ”是“函数
”是“函数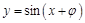 的图象关于y轴对称”的
的图象关于y轴对称”的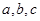 ,若
,若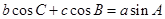 ,则△ABC的形状为( )
,则△ABC的形状为( )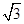 ).
).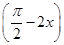 -2f2(x)在区间
-2f2(x)在区间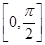 上的值域.
上的值域.