题目内容
已知
=(1,cosx),
=(
,sinx),x∈(0,π)
(1)若
∥
,求
的值;
(2)若
⊥
,求sinx-cosx的值.
| a |
| b |
| 1 |
| 3 |
(1)若
| a |
| b |
| sinx+cosx |
| sinx-cosx |
(2)若
| a |
| b |
(1)∵a∥b⇒sinx=
cosx⇒tanx=
∴
=
=
=-2
(2)∵a⊥b⇒
+sinxcosx=0⇒sinxcosx=-
∴(sinx-cosx)2=1-2sinxcosx=
又∵x∈(0,π)且sinxcosx<0⇒x∈(
,π)⇒sinx-cosx>0
∴sinx-cosx=
| 1 |
| 2 |
| 1 |
| 3 |
∴
| sinx+cosx |
| sinx-cosx |
| tanx+1 |
| tanx-1 |
| ||
|
(2)∵a⊥b⇒
| 1 |
| 3 |
| 1 |
| 3 |
∴(sinx-cosx)2=1-2sinxcosx=
| 5 |
| 3 |
又∵x∈(0,π)且sinxcosx<0⇒x∈(
| π |
| 2 |
∴sinx-cosx=
| ||
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -2x)+sin2x
-2x)+sin2x

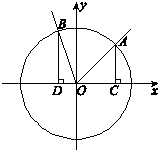
 则
则 .
.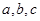 ,若
,若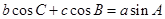 ,则△ABC的形状为( )
,则△ABC的形状为( )