Question

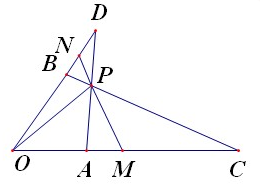
在平面直角坐标系中，N为圆C：（x+1）²+y²=16上的一动点，点D（1，0），点M是DN的中点，点P在线段CN上，且

MP

•

DN

=0．
（Ⅰ）求动点P表示的曲线E的方程；
（Ⅱ）若曲线E与x轴的交点为A，B，当动点P与A，B不重合时，设直线PA与PB的斜率分别为k₁，k₂，证明：k₁•k₂为定值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）根据由点M是DN的中点，

MP

•

DN

=0，结合|PC|+|PN|=|CN|，可得|PC|+|PD|=4，由椭圆定义知，点P的轨迹是以C，D为焦点的椭圆，从而可求动点P表示的曲线E的方程；
（Ⅱ）分别求出k₁，k₂，利用椭圆方程，即可证明．

解答： （Ⅰ）解：由点M是DN的中点，

MP

•

DN

=0，可知PM垂直平分DN．
所以|PN|=|PD|，
又|PC|+|PN|=|CN|，所以|PC|+|PD|=4．
由椭圆定义知，点P的轨迹是以C，D为焦点的椭圆．----------------------（4分）
设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)．
又2a=4，2c=2，可得a²=4，b²=3．
所以动点P表示的曲线E的方程为

x2

4

+

y2

3

=1．----------------------（6分）
（Ⅱ）证明：易知A（-2，0），B（2，0）．
设P（x₀，y₀）（y₀≠0），则

x 2 0

4

+

y 2 0

3

=1，即

y

2 0

=3(1-

x 2 0

4

)，
则k1=

y0

x0+2

，k2=

y0

x0-2

，----------------------（8分）
即k1•k2=

y 2 0

x 2 0 -4

=

3(1- x 2 0 4 )

x 2 0 -4

=

- 3 4 ( x 2 0 -4)

x 2 0 -4

=-

3

4

，
∴k₁•k₂为定值-

3

4

．-----------------------------------12

点评：本题考查椭圆的标准方程，椭圆的定义，斜率的计算，考查学生分析解决问题的能力，属于中档题．