题目内容
已知f(x)=x2-2x,则在下列区间中,y=f(x)一定有零点的是( )
| A、(-3,-2) |
| B、(-1,0) |
| C、(2,3) |
| D、(4,5) |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据f(x)=x2-2x是R上的连续函数,f(-1)<0,f(0)>0,可得函数f(x)在(-1,0)上有零点,从而得出结论.
解答:
解:根据f(x)=x2-2x是R上的连续函数,f(-1)=
>0,f(0)=-1<0,
可得函数f(x)在(-1,0)上有零点,
故选:B
| 1 |
| 2 |
可得函数f(x)在(-1,0)上有零点,
故选:B
点评:本题主要考查函数的零点的判定定理的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆
+
=1的一个焦点为(2,0),则椭圆的方程是( )
| x2 |
| a2 |
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、x2+
| ||||
D、
|
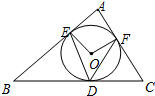 如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )| A、40° | B、55° |
| C、65° | D、70° |
用二分法求方程lnx+2x=6的近似解(精度0.01),先令f(x)=lnx+2x-6,则根据下表数据,方程的近似解可能是( )
| x | 2 | 3 | 2.5 | 2.75 | 2.625 | 2.5625 | 2.53125 | 2.546875 | 2.5390625 |
| f(x)近似值 | -1.31 | 0.69 | -0.84 | 0.52 | 0.215 | 0.0666 | -0.009 | 0.029 | 0.010 |
| A、2.512 |
| B、2.522 |
| C、2.532 |
| D、2.542 |
若复数
(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| a-2i |
| 1+i |
| A、2 | B、-2 | C、1 | D、-1 |
执行如图所示的程序框图,如果输出2,那么判断框内应填入的条件是( )


| A、k≤3? | B、k≤4? |
| C、k>3? | D、k>4? |
若a-2i=b+ai,其中a、b∈R,i是虚数单位,则a+b=( )
| A、-4 | B、4 | C、0 | D、数值不定 |
复数z=
,则
=( )
| 2 |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
 将连续整数1,2,…,25填入如图所示的5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为
将连续整数1,2,…,25填入如图所示的5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为