题目内容
设集合A={x|x2+2x-3≤0}，Z为整数集，则A∩Z=（ ）
| A、{x|-3＜x＜1} |
| B、{x|-3≤x≤1} |
| C、{-2，-1，0} |
| D、{-3，-2，-1，0，1} |
考点：交集及其运算
专题：集合
分析：求出集合的元素，根据集合的基本运算即可得到结论．
解答：
解：A={x|x2+2x-3≤0}={x|-3≤x≤1}，∵Z为整数集，则A∩Z={-3，-2，-1，0，1}，故选：D
点评：本题主要考查集合的基本运算，比较基础．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数f（x）=log2x，且函数y=g（x）的图象与函数y=f（x）的图象关于直线y=x对称，则函数g（x2）是（ ）
| A、奇函数且在（0，+∞）上是减函数 |
| B、偶函数且在（0，+∞）上是增函数 |
| C、奇函数且在（-∞，0）上是减函数 |
| D、偶函数且在（-∞，0）上是增函数 |
下列集合的表示方法正确的是（ ）
| A、{1，2，3，3，} |
| B、{全体有理数} |
| C、0={0} |
| D、不等式x-3＞2的解集是{x|x＞5} |
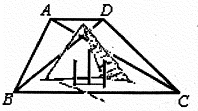如图，在一座底部不可到达的孤山两侧，有两段平行的公路AB和CD，现测得AB=5，AC=9∠BCA=30°，∠ADB=45°若函数f（x）=-
x2+bx+1在[-1，+∞）上是减函数，则b的取值范围是（ ）
| 1 |
| 2 |
| A、[-1，+∞） |
| B、（-1，+∞） |
| C、（-∞，-1） |
| D、（-∞，-1] |