题目内容
10.已知抛物线C:y2=2px(p>0)的焦点为F,过F的直线交抛物线C于A,B两点,以线段AB为直径的圆与抛物线C的准线切于$M(-\frac{p}{2},3)$,且△AOB的面积为$\sqrt{13}$,则抛物线C的方程为y2=4x.分析 求出直线AB的方程,利用△AOB的面积为$\sqrt{13}$,建立方程求出p,即可求出抛物线C的方程.
解答 解:令A(x1,y1)B(x2,y2),
由已知以AB为直径的圆相切于$M(-\frac{p}{2},3)$,∴y1+y2=6,
A,B代入抛物线方程,作差可得kAB=$\frac{p}{3}$,
设直线AB的方程为y=$\frac{p}{3}$(x-$\frac{p}{2}$),
与抛物线方程联立可得y2-6y-p2=0,∴y1y2=-p2,
∵△AOB的面积为$\sqrt{13}$,
∴$\frac{1}{2}×\frac{p}{2}×$|y1-y2|=$\sqrt{13}$,
∴p$\sqrt{36+4{p}^{2}}$=4$\sqrt{13}$,∴p=2,
∴抛物线C的方程为y2=4x,
故答案为:y2=4x.
点评 本题考查抛物线的方程与性质,考查圆的方程,考查学生的计算能力,属于中档题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
20.执行如图的程序框图,若输入的n为6,则输出的p为( )
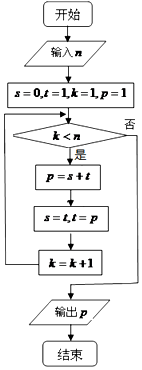

| A. | 8 | B. | 13 | C. | 29 | D. | 35 |
5.把函数f(x)=2sin(x+2φ)(|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{2}$个单位长度之后,所得图象关于直线$x=\frac{π}{4}$对称,且f(0)<f($\frac{π}{2}$-φ),则φ=( )
| A. | $\frac{π}{8}$ | B. | $\frac{3π}{8}$ | C. | $-\frac{π}{8}$ | D. | $-\frac{3π}{8}$ |
2.已知函数f(x)=|log2|1-x||,若函数g(x)=f2(x)+af(x)+2b有6个不同的零点,则这6个零点之和为( )
| A. | 7 | B. | 6 | C. | $\frac{11}{2}$ | D. | $\frac{9}{2}$ |