题目内容
18．已知集合A={1，2，4}，集合$B=\{z|z=\frac{x}{y}，x∈A，y∈A\}$，则集合B中元素的个数为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 根据条件列举即可．
解答 解：∵A={1，2，4}，
∴集合$B=\{z|z=\frac{x}{y}，x∈A，y∈A\}$={1，$\frac{1}{2}$，$\frac{1}{4}$，2，4}
∴集合B中元素的个数为5个，
故选B．
点评 本题考查了集合的运算的变形应用，属于基础题．
练习册系列答案
相关题目
8．运行如图所示的程序框图，则输出的a、b、c满足（ ）
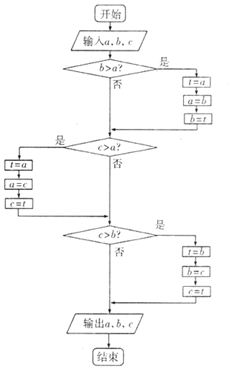
| A． | c≤b≤a | B． | a≤b≤c | C． | a≤c≤b | D． | b≤c≤a |
13．若不等式|x-t|＜1成立的必要条件是1＜x≤4，则实数t的取值范围是（ ）
| A． | [2，3] | B． | （2，3] | C． | [2，3） | D． | （2，3） |
3．已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右焦点为F，过F作双曲线C渐近线的垂线，垂足为A，且交y轴于B，若$\overrightarrow{BA}=2\overrightarrow{AF}$，则双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{6}}}{2}$ |
7．2017年某市开展了“寻找身边的好老师”活动，市六中积极行动，认真落实，通过微信关注评选“身边的好老师”，并对选出的班主任工作年限不同的五位“好老师”的班主任的工作年限和被关注数量进行了统计，得到如下数据：
（1）若”好老师”的被关注数量y与其班主任的工作年限x满足线性回归方程，试求回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，并就此分析：“好老师”的班主任工作年限为15年时被关注的数量；
（2）若用$\frac{y_i}{x_i}$（i=1，2，3，4，5）表示统计数据时被关注数量的“即时均值”（四舍五入到整数），从“即时均值”中任选2组，求这2组数据之和小于8的概率．（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．
| 班主任工作年限x（单位：年） | 4 | 6 | 8 | 10 | 12 |
| 被关注数量y（单位：百人） | 10 | 20 | 40 | 60 | 50 |
（2）若用$\frac{y_i}{x_i}$（i=1，2，3，4，5）表示统计数据时被关注数量的“即时均值”（四舍五入到整数），从“即时均值”中任选2组，求这2组数据之和小于8的概率．（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．
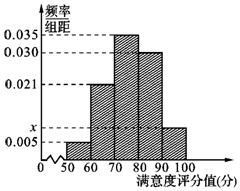共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务，由于其依托“互联网+”，符合“低碳出行”的理念，已越来越多地引起了人们的关注．某部门为了对该城市共享单车加强监管，随机选取了100人就该城市共享单车的推行情况进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照[50，60），[60，70），…，[90，100]分成5组，制成如图所示频率分直方图．