题目内容
如图,三棱柱ABC-A1B1C1的底面是边长为3的正三角形,侧棱AA1垂直于底面ABC,AA1=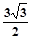 ,D是CB延长线上一点,且BD=BC.
,D是CB延长线上一点,且BD=BC.
(1)求证:直线BC1∥平面AB1D;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积。
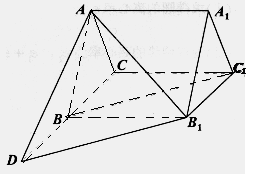
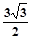 ,D是CB延长线上一点,且BD=BC.
,D是CB延长线上一点,且BD=BC.(1)求证:直线BC1∥平面AB1D;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积。

(I)
 ,又
,又 ,
, 四边形
四边形 是平行四边形,
是平行四边形,  。
。又
 平面
平面 ,
, 平面
平面 ,
, 直线
直线 平面
平面
(Ⅱ)过
 作
作 于
于 ,连结
,连结
 平面
平面 ,
, ,
, 是二面角
是二面角 的平面角。
的平面角。 ,
, 是
是 的中点,
的中点, 。
。在
 中,
中, 
 ,即二面角
,即二面角 的大小为60°
的大小为60°Ⅲ)过
 作
作 于
于 ,
, 平面
平面 ,
, 平面
平面 平面
平面 ,
, 平面
平面 且
且 为点
为点 到平面
到平面 的距离。
的距离。 ,
, 。
。分析:(1)根据三棱柱的性质,可以证出BC
 ∥DB
∥DB ,结合线面平行的判定定理可以证出直线BC
,结合线面平行的判定定理可以证出直线BC ∥平面AB1D;
∥平面AB1D;(2)过B作BE⊥AD于E,连接EB
 ,根据三垂线定理得∠B
,根据三垂线定理得∠B EB是二面角B
EB是二面角B -AD-B的平面角.在Rt△BB
-AD-B的平面角.在Rt△BB E中,利用三角函数的定义可算出∠B1EB=60°,即二面角B
E中,利用三角函数的定义可算出∠B1EB=60°,即二面角B -AD-B的大小为60°.
-AD-B的大小为60°.(3)过A作AF⊥BC于F,利用面面垂直的性质定理,可得AF⊥平面BB
 C
C C,即AF等于点A到平面B
C,即AF等于点A到平面B C
C B的距离.利用等边三角形计算出AF的长为
B的距离.利用等边三角形计算出AF的长为  ,结合三角形B
,结合三角形B C
C B的面积等于
B的面积等于  ,用锥体体积公式可以算出三棱锥C
,用锥体体积公式可以算出三棱锥C -ABB
-ABB 的体积.
的体积.解答:解:(1)∵CB∥C
 B
B ,且BD=BC=B
,且BD=BC=B C
C ,
,∴四边形BDB
 C
C 是平行四边形,可得BC
是平行四边形,可得BC ∥DB
∥DB .
.又B
 D?平面AB1D,BC
D?平面AB1D,BC ?平面AB
?平面AB D,
D,
∴直线BC
 ∥平面AB
∥平面AB D
D(2)过
 作
作 于
于 ,连结
,连结
 平面
平面 ,
, ,
, 是二面角
是二面角 的平面角。
的平面角。 ,
, 是
是 的中点,
的中点, 。
。在
 中,
中, 
 ,即二面角
,即二面角 的大小为60°
的大小为60°(3)过
 作
作 于
于 ,
, 平面
平面 ,
, 平面
平面 平面
平面 ,
, 平面
平面 且
且 为点
为点 到平面
到平面 的距离。
的距离。 ,
, 。
。点评:本题以一个特殊正三棱柱为载体,适当加以变化,求三棱锥的体积并求二面角的大小,着重考查了空间线面平行的判定、面面垂直的判定与性质等知识点,属于中档题.

练习册系列答案
相关题目
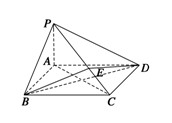
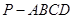 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱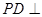 底面ABCD,
底面ABCD,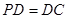 ,E是PC的中点,作
,E是PC的中点,作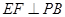 交PB于点F.
交PB于点F.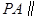 平面
平面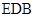 ;
;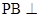 平面EFD;
平面EFD;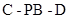 的大小.
的大小.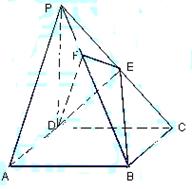
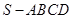 的底面是正方形,
的底面是正方形,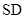 ⊥平面
⊥平面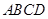 ,
,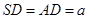 ,点E是SD上的点,且
,点E是SD上的点,且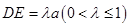 .
.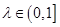 ,都有AC⊥BE;
,都有AC⊥BE;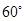 ,求
,求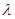 的值.
的值.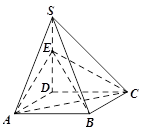
 中,
中, 面
面 ,底面
,底面 分别是
分别是 的中点,
的中点, ,
, 面
面 ;
; 面
面 ;
;

 的长方体被截面
的长方体被截面 所截而得到的,其中
所截而得到的,其中 .
. ;
; 到平面
到平面
 ,则
,则 的取值范围是( )
的取值范围是( )





 的面积。
的面积。